SOLUTION: i dont know how do 30 60 90 triangles that already have one side and also 45 45 90 triangles and sin-1 and all that please help.

A 30°-60°-90° is found by starting with an equilateral triangle, like this,
where all the sides are equal and all the angles equal 60°:

 

Then we cut it in two:

 

That makes the angles at the top be 30° each because they are half of
a 60° angle, and it makes two 90° angles at the bottom like this:



Now we throw away the right half and keep the left half, like this:



That is a 30°-60°-90° right triangle.  It is half of an equilateral 
triangle.  Now since the original equilateral triangle had all three 
sides equal, that means that in a 30°-60°-90° right triangle, the 
bottom side (the shrtest side) is exactly one-half of the hypotenuse,
which is the slanted side.  Or equivalently, the hypotenuse or the
slanted side is exactly twice as long as the bottom (or shortest) side.

So the important thing about a 30°-60°-90° right triangle is that its 
LONGEST side is TWICE its shortest side.

It is customary to say that the shortest side (bottom side) is 1
unit long, and its hypotenuse (longest side) is 2 units long.  Like this:



Now we need to find the length of the middle-sized side, which is the
vertical side.  To find that we'll use the Pythagorean theorem:

       a² + b² = c²

We will let "a" be the shortest side, 1, and "c" be the longest side 2,
and find "b", the middle, sibstituting:

     (1)² + b² = (2)²

        1 + b² = 4

Subtract 1 from both sides:

            b² = 3  

Take square roots of both sides of the equation:
                  _
             b = Ö3
                                      _ 
So we label the middle-sized side as Ö3



and now the 30°-60°-90° right triangle is complete, for
we know all three angles and all three sides, and all
three angles,

Now be sure to memorize this important triangle, its angles and its
sides, because from it you can get all the trigonometric ratios for
both 30° and 60°, which are very important angles.  In fact they are
called SPECIAL angles.

Looking at the triangle above, and remembering the definitions of the
sine, cosine, tangent, secant, cosecant, and cotangent, we see that

sin(60°) =  = 
cos(60°) =  = 
tan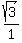(60°) =  =  = 
sec(6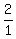0°) =  =  = 2
csc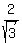(60°) =  =  = 
cot(60°) =  =  = 

sin(30°) =  = 
cos(30°) =  = 
tan(30°) =  =  = 
sec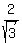(30°) =  =  = 
csc(3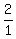0°) =  =  = 2
cot(30°) =  =  =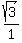 

Also, be sure that you can recognize this triangle when it is draw as above,
but also be sure you can recognize it when it is lying on its side like any
of these:




Tommorrow  I'll post you an equally interesting story about the 45°-45°-90°
right triangle.  But try to absorb this one.

Edwin

A 45°-45°-90° is found by starting with a square, like this,
where all the sides are equal and all the angles equal 90°:

 

Then we cut it in two, with a diagonal:



That makes the angles at the upper right and lower left to be 45° 
each because they are half of a 90° angle, and it makes two 45° angles 
at the lower left and upper right:



Now we throw away the top half and keep the bottom half, like this:



That is a 45°-45°-90° right triangle.  It is half of a square. Now 
since the original square had all four sides equal, that means that in 
a 45°-45°-90° right triangle, the bottom side is exactly equal to the
right side. That means that the important thing about a 45°-45°-90° right triangle is that it is an isosceles right triangle.

It is customary to say that the two equal sides are 1 unit each. Like this:



Now we need to find the length of the longest side, or hypotenuse, which is 
the slanted side.  To find that we'll use the Pythagorean theorem:

       a² + b² = c²

We will let "a" be the bottom side, 1, and "b" be the right side, also 1,
and find "c", the hypotenuse. Substituting:

     (1)² + (1)² = c²

           1 + 1 = c²

               2 = c²

              Take square roots of both sides of the equation:
               _
              Ö2 = c
                               _ 
So we label the hypotenuse as Ö2




and now the 45°-45°-90° right triangle is complete, for
we know all three angles and all three sides, and all
three angles,

Now be sure to memorize this important triangle, its angles and its
sides, because from it you can get all the trigonometric ratios for
45°, which is a very important angles.  It is one of the angles known
as SPECIAL angles.

Looking at the triangle above, and remembering the definitions of the
sine, cosine, tangent, secant, cosecant, and cotangent, we see that

sin(45°) =  =  = 
cos(45°) =  =  = 
tan(45°) =  =  = 1
sec(45°) =  =  = 
csc(45°) =  =  = 
cot(45°) =  =  = 1

Edwin