|
Question 558739: What is the vertex, focus, axis of symmetry, and directiv of the following equation, (x-2)² = y+3 and how did you get those answers?
Found 2 solutions by KMST, Edwin McCravy:
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! The equation is the equation of a parabola in vertex form.
VERTEX
The coordinates of the vertex are shown in the equation subtracted from the  and the and the  . .
The vertex is (2,-3).
The vertex has  <---> <--->  and and  <---> <--->  , and , and  . .
It is a minimum, because, for any value of  other than other than  , , 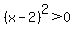 , making , making  <---> <--->  . .
AXIS OF SYMMETRY
For all points other than the vertex, the same value of  happens for two different values of happens for two different values of  , at equal distances to the left and right of the line , at equal distances to the left and right of the line  <---> <--->  . That line is the axis of symmetry. . That line is the axis of symmetry.
FOCUS AND DIRECTRIX
The focus is the point (2,-3+c) above the vertex/minimum that the parabola "wraps" around. The directrix is the line  at the same distance on the other side of the vertex. at the same distance on the other side of the vertex.
Your book will tell you that the coefficient of  in the equation equals in the equation equals 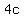 , so in this case , so in this case  --> --> 
The focus has  . It is the point (2,-11/4). . It is the point (2,-11/4).
The directrix is the line  --> -->  . .
Answer by Edwin McCravy(20055)   (Show Source): (Show Source):
You can put this solution on YOUR website!
The standard form of a parabola whose axis is symmetry is vertical is
(x - h)² = 4p(y - k) [Some books use "a" or "c" instead of "p"]
Where (h,k) is the vertex. |p| is the diatance from the vertex to
the focus (which is a point inside the parabola on its axis of symmetry),
and also to the directrix, which is a line outside the parabola
perpendicular to its line of symmetry. If p is positive the parabola
opens upward, and if p is negative it opens downward.
We compare your equation to that one:
(x - 2)² = y + 3
To get it looking like
(x - h)² = 4p(y - k)
we put parentheses around the right side and a 1 infront
(x - 2)² = 1(y + 3)
So we see that h = 2, k = -3, and 4p = 1 which makes p =  So the vertex is (h,k) = (2,-3).
We plot the vertex (2,-3), and draw a green axis of symmetry through
it.
So the vertex is (h,k) = (2,-3).
We plot the vertex (2,-3), and draw a green axis of symmetry through
it.
 That green axis of symmetry goes through x = 2, so that's its equation.
The vertex is a point p or
That green axis of symmetry goes through x = 2, so that's its equation.
The vertex is a point p or  of a unit above the vertex. It is
on the axis of symmetry so it's x-coordinate is the same as the x-coordinate
of the vertex, which is 2, but its y-coordinate is of a unit above the vertex. It is
on the axis of symmetry so it's x-coordinate is the same as the x-coordinate
of the vertex, which is 2, but its y-coordinate is  of a unit
more, so we add of a unit
more, so we add  to the y-coordinate of the vertex:
-3+ to the y-coordinate of the vertex:
-3+ = = 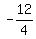 + + = =  ,
So the focus has the coordinates (2, ,
So the focus has the coordinates (2, )
We draw the focus: )
We draw the focus:
 The directrix is a horizontal line p or
The directrix is a horizontal line p or  of a unit below the vertex
We draw it in blue: of a unit below the vertex
We draw it in blue:
 Since the line is
Since the line is  unit below the vertex, we subtract unit below the vertex, we subtract  from
its y-coordinate -3- from
its y-coordinate -3- = = 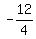 - - = =  ,
so the equation of the directrix is y = ,
so the equation of the directrix is y =  We draw two adjacent squares, with a common side from the directrix
to the focus, like this:
We draw two adjacent squares, with a common side from the directrix
to the focus, like this:
 and sketch in the parabola through the upper corners of those squares and
through the vertex:
and sketch in the parabola through the upper corners of those squares and
through the vertex:
 Edwin
Edwin
|
|
|
| |