|
Question 558697: (y+1)^(2)=-8(x-3)
vertex: ?
focus point: ?
equation of the axis of symmetry: ?
equation of directrix: ?
2 random points on equation: ?
IN NEED OF HELP!!! PLEEEEASE HELP ME ON THIS PROBLEM, I AM REALLY STUCK ON IT AND TRY TO GET BACK WITH ANSWERS ASAP! THANK YOU ONCE AGAIN!
Found 2 solutions by stanbon, KMST:
Answer by stanbon(75887)   (Show Source): (Show Source):
You can put this solution on YOUR website! (y+1)^(2)=-8(x-3)
vertex: ?
focus point: ?
equation of the axis of symmetry: ?
equation of directrix: ?
2 random points on equation: ?
------
Rearrange the equation:
-8x+24 = (y+1)^2
---
-8x = (y+1)^2 - 24
x = (-1/8)(y+1)^2 + 3
This is a parabola opening to the left.
--------
vertex: (3,-1)
-------------------
focus point:
4p = -1/8
p = -1/32
focus: (3-(1/32),-1)
-----------------------
equation of the axis of symmetry: y = -1
------------------------
equation of directrix: x = 3+(1/32)
-------------------------
2 random points on equation:
-8x+24 = (y+1)^2
---
Let x = 1, then (y+1)^2 = 16, then y =3 or y = -6
Let x = 5/2, then (y+1)^2 = 4, then y = 1 or y = -3
===========================================================
Cheers,
Stan H.
===========
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! The equation  is the equation of a parabola in vertex form. In that form, the equation shows you the coordinates of the vertex. They are subtracted from the is the equation of a parabola in vertex form. In that form, the equation shows you the coordinates of the vertex. They are subtracted from the  and the and the  ). The location of the directrix and the focus point can be calculated from the coefficient ). The location of the directrix and the focus point can be calculated from the coefficient  in the equation. in the equation.
Your book tells you all about it, but you can figure it all out without the book, and without memorizing any formulas.
VERTEX AND AXIS OF SYMMETRY
What happens when  <---> <--->  ? ?
 ---> --->  ---> ---> 
The fact that both parenteses are zero tells you that it is a very special point.
For any other value of  , ,  ---> ---> 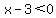 ---> ---> 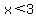
So,  , no matter what value y takes. It's a maximum value for x. Point (3,-1) is the vertex, and , no matter what value y takes. It's a maximum value for x. Point (3,-1) is the vertex, and  is the axis of symmetry. is the axis of symmetry.
TWO RANDOM POINTS
Let's try  <---> <---> 
 ---> --->  ---> ---> 
Let's try  <---> <---> 
 ---> --->  ---> ---> 
DIRECTRIX AND FOCUS POINT
The directrix will be  and the focus will be at (3-c,-1) and the focus will be at (3-c,-1)
The points on the parabola for  will be at a distance will be at a distance
 , measured vertically, above and below the focus point. , measured vertically, above and below the focus point.
They will also be at a distance 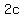 measured horizontally from the directrix. measured horizontally from the directrix.
By the definition of parabola, those distances are the same, so
 --> -->  --> --> 
On the other hand, from the equation given,  , we know that for , we know that for 
 --> --> 
Substituting that expression for 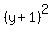 in in  we get we get
 --> -->  --> -->  is the solution we need. is the solution we need.
The directrix is  --> --> 
Thee focus point has  , so it's the point (1,-1). , so it's the point (1,-1).
|
|
|
| |