SOLUTION: One pump fills a tank two times as fast as another pump. If the pumps work together they fill the tank in 18 minutes. How long does it take each pump working alone to fill the tank

Algebra ->  Rate-of-work-word-problems -> SOLUTION: One pump fills a tank two times as fast as another pump. If the pumps work together they fill the tank in 18 minutes. How long does it take each pump working alone to fill the tank      Log On


   

Question 558604: One pump fills a tank two times as fast as another pump. If the pumps work together they fill the tank in 18 minutes. How long does it take each pump working alone to fill the tank?

Answer by Edwin McCravy(20054) About Me  (Show Source):
You can put this solution on YOUR website!
One pump fills a tank two times as fast as another pump. If the pumps work together they fill the tank in 18 minutes. How long does it take each pump working alone to fill the tank?
Make this chart:
================================================================
                       number of       number of     rate in
                      tanks filled      minutes    tanks/minute
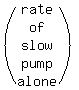
Slow pump alone          

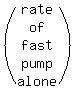
Fast pump alone            

Both pumps together
================================================================

Let the time for the fast pump to fill one tank be x minutes.

Fill in 1 for the number of tanks and x for the number of minutes
for the fast pump alone:

================================================================
                       number of       number of     rate in
                      tanks filled      minutes    tanks/minute
Slow pump alone            

Fast pump alone            1                x

Both pumps together
================================================================

>>...One pump fills a tank two times as fast as another pump...<<
Since the slow pump takes twice as long as the fast pump, its time
to fill one tank is 2x minutes.

Fill in 1 for the number of tanks and 2x for the number of minutes
for the slow pump alone:

================================================================
                       number of       number of     rate in
                      tanks filled      minutes    tanks/minute
Slow pump alone            1               2x

Fast pump alone            1                x

Both pumps together
================================================================

>>...If the pumps work together they fill the tank in 18 minutes...<<
Fill in 1 for the number of tanks and 18 for the number of minutes
for both pumps pumping together:


================================================================
                       number of       number of     rate in
                      tanks filled      minutes    tanks/minute
Slow pump alone            1               2x

Fast pump alone            1                x

Both pumps together        1               18
================================================================

Now we fill in the rates in tank/minute by dividing the number of
tanks filled by the number of minutes:

================================================================
                       number of       number of     rate in
                      tanks filled      minutes    tanks/minute
Slow pump alone            1               2x 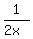        expr%281%2F%282x%29%29
Fast pump alone            1                x          1%2Fx 
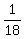Both pumps together        1               18          1%2F18
================================================================

The equation comes from

                      %28matrix%285%2C1%2Crate%2C+of%2C+slow%2C+pump%2C+alone%29%29 + %28matrix%285%2C1%2Crate%2C+of%2C+fast%2C+pump%2C+alone%29%29 = %28matrix%285%2C1%2Crate%2C+of%2C+both%2C+pumps%2C+together%29%29

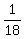                            1%2F%282x%29 + 1%2Fx = 1%2F18

          Multiply through by LCD of 18x and solve

            Solution x = 27 minutes for the fast pump to fill 1 tank.
                    2x = 2(27) = 54 minutes for the slow pump to fill 1 tank. 


Edwin