Question 557798: For a normally distributed population, mean of 6.5 and standard
deviation of 4, compute:
a. The probability of picking one item from the population and having it fall between 6.5 and 14.75
Answer by Edwin McCravy(20060)   (Show Source):
You can put this solution on YOUR website! For a normally distributed population, mean of 6.5 and standard
deviation of 4, compute:
a. The probability of picking one item from the population and having it fall between 6.5 and 14.75
z-score for left endpoint 6.5 is = 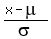 =  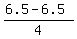= 0
(1) if your z-table reads from the middle, look up z=0, get 0
(2) if your z-table reads from the left, look up z=0, get 0.5
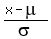z-score for right endpoint 14.75 is =  = 2.0625, round to 2.06
(1) if your z-table reads from the middle, look up 2.06, get .4803
(2) if your z-table reads from the left, look up 2.06, get .9803
(1) if your z-table reads from the middle, subtract .4803-0 = .4803
(2) if your z-table reads from the left, subtract .9803-.5 = .4803
Answer: .4803
Edwin
|
|
|
