Question 557526: Another problem. Please help. My last question was nicely solved by stanbon(47716) and I salute you. the question is:-
When the expression a^+bx+c is divided by x-2, the remainder is R. When the expression is divided by x+1, the remainder is still R.
i.) Find the value of b.
ii.) When the expression is divided by x-4, the remainder is 2R. Find the value of c and R.
iii.) When the expression is divided by x-t, the remainder is 5R. Find the two possible values of t.
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! i.
I suspect you mean
"When the expression C is divided by x-2, the remainder is R. When the expression is divided by x+1, the remainder is still R."
You have a quadratic trinomial 
When you divide a polynomial P(x) by (x-a), the original polynomial, P(x), the quotient polynomial, Q(x), and the remainder R, are related through:
P(x)=Q(x)(x-a)+R (and P(a)=R).
So,
P(x)-R = Q(x)(x-a) is divisible by x-a.
In the case of your polynomial, P(x)-R is divisible by x-2 and by x+1.
So it is divisible by

Then  and and

So 
ii.
P(4) = 
 --> --> 

iii.
P(t) = 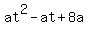 = = 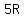 = = 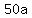
 --> --> 
Factoring, we get 
so  has solutions has solutions 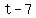 and and 
|
|
|