|
Question 557426: I don't think that this cubic polynomial can be factored, but I don't know how to prove it. All methods I can think of to factor the polynomial have failed. How can I be sure that there is no way to factor this polynomial?
9x^3 + 5x^2 - 8
Answer by bucky(2189)   (Show Source): (Show Source):
You can put this solution on YOUR website! Is this a math exercise or something that you are trying to solve to simplify a real-world problem? The reason that I ask you to think about that question is because this given expression of:
.
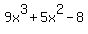
.
can be factored, but it is not a "nice" conventional answer with an integer. That is to say, it's not a factor like (x + 1) or (x - 7) or something similarly as ordinary as those examples.
.
How do I know? Here's what I did. I used a graphing calculator to make a graph of the function:
.

.
It crosses the x-axis once at a value of x equal to approximately +0.8. (I'll refine that a little bit later.) Since that value of x is a point on the x-axis, it has a corresponding value of y = 0, and is, therefore, a value of x that satisfies the equation:
.

.
This means that there is a factor of approximately (x - 0.8) that multiplies the terms that remain on the right side after (x - 0.8) is factored out. Then, when x reaches +0.8 it makes the factor (x - 0.8) go to zero and multiplying the other terms left on the right side by that zero makes the entire right side equal zero. This would demonstrate that it indeed is a factor.
.
Since the graph crosses the x-axis (while rising as x moves to the right) there must be a point on the x-axis where the corresponding value of y is exactly zero. I set about choosing values of x slightly greater than 0.8. If the value of x that I chose was too large, I could tell because when that value of x was substituted into  it would result in a value of y that was positive (greater than zero). So I would select a slightly smaller value of x. If it was still too large, it too would result in a value of y that, while smaller and closer to zero, was still positive and greater than zero. I would keep decreasing x and trying it until it got small enough to result in a value of y that was negative, meaning that x was now too small. So I would increase x slightly until it eventually resulted in a value of y that was positive. I kept increasing and decreasing x, all the while I was narrowing in on getting a value for y that was closer and closer to zero. it would result in a value of y that was positive (greater than zero). So I would select a slightly smaller value of x. If it was still too large, it too would result in a value of y that, while smaller and closer to zero, was still positive and greater than zero. I would keep decreasing x and trying it until it got small enough to result in a value of y that was negative, meaning that x was now too small. So I would increase x slightly until it eventually resulted in a value of y that was positive. I kept increasing and decreasing x, all the while I was narrowing in on getting a value for y that was closer and closer to zero.
.
This iterative process reached the point that x was +0.807535042914037 and the corresponding value of y for this value of x was
.
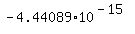 or or 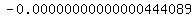
.
Not zero, but pretty close to it. So I could now say that
.
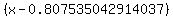
.
was a very close approximation of the factor. (Not close enough for a "correct" answer in mathematical terms, but most likely significantly more accuracy than needed for real world engineering problems.)
.
So there you are. You are correct in saying that the expression you were given does not factor exactly. But since the graph crosses the positive x-axis there has to be at least one number (most likely irrational - non-terminating) where that value for x will allow you to declare that (x - that number) is a factor.
.
And since the graph of:
.

.
only crosses the x-axis at one point, this is the only point where a real root exists. If the quadratic that remains after you divide out the real factor will therefore likely have just a pair of complex roots, meaning that its two roots consist of a complex (meaning real and imaginary parts) conjugate pair of numbers). You can use the quadratic formula to find those two roots.
.
I hope this didn't confuse you too much, but it may give you a little insight into the problem you are trying to resolve.
.
|
|
|
| |