|
Question 557410: The denominator of a fraction is 2 less than twice the numerator. If 4 is added to both the numerator and the deniminator, we obtain a fraction equivalent to 5/8. What is the original fraction? How do we represent it?
Answer by bucky(2189)   (Show Source): (Show Source):
You can put this solution on YOUR website! Start by letting N represent the numerator and D represent the denominator.
.
You are told that the denominator is twice the numerator less 2. Therefore, you can write this denominator as:
.

.
So you now can write the fraction (numerator divided by denominator) as:
.
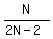
.
Next you are told that if you add 4 to both the numerator and the denominator, you will get a fraction that can be reduced to 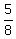 . When you add 4 to both the numerator and the denominator, this fraction becomes: . When you add 4 to both the numerator and the denominator, this fraction becomes:
.
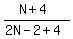
.
In the denominator the -2 and the +4 combine to give +2. This simplification reduces this fraction to:
.

.
And this simplified fraction is to equal 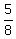 . So set it equal to . So set it equal to 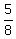 and you have the equation: and you have the equation:
.

.
Notice that this is a proportion (two fractions equal to each other). You can solve proportions by multiplying the numerator on the right side times the denominator on the left side, and setting this product equal to the product that you get by multiplying the numerator on the left side times the denominator on the right side. (A common term for this process is "cross-multiplication" because if you draw lines from the numerator on one side through the denominator on the other side, the two lines cross through the equal sign. The two resulting products are called "cross-products" for the same reason.)
.
The product of the numerator on the right side times the denominator on the left side is:
.
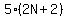 and this product is and this product is 
.
and the product of the numerator on the left side times the denominator on the right side is:
.
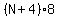 and this product is and this product is 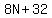
.
To solve for N you start by setting these two cross-products equal as follows:
.
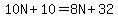
.
Subtract 8N from both sides to get rid of the term containing N on the right side. As a result of subtracting 8N from both sides, the 8N on the right side disappears, and the 10N minus 8N on the left side results in 2N. So the equation is simplified to:
.

.
Next, subtract 10 from both sides and the resulting equation is:
.

.
Finally, divide both sides by 2 and you find that N, the numerator of the original fraction, is:
.

.
Since the denominator (D) of the original fraction was 2N -2, if N is equal to 11, you know that the denominator is given by:
.

.
and the denominator simplifies to 
.
The fraction you were to find is:
.

.
You can check this by adding 4 to both the numerator and the denominator to get:
.

.
and if you divide both 15 and 24 by 3, you find that this fraction is 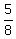 just as it is supposed to be. So the answer we got for the fraction being: just as it is supposed to be. So the answer we got for the fraction being:
.
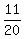
.
checks.
.
Hope this helps you to understand this problem.
.
|
|
|
| |