SOLUTION: The sum of the reciprocals of two consecutive odd integers is 8/15. Find the integers. Thank you.

Algebra ->  Percentage-and-ratio-word-problems -> SOLUTION: The sum of the reciprocals of two consecutive odd integers is 8/15. Find the integers. Thank you.      Log On


   

Question 55652: The sum of the reciprocals of two consecutive odd integers is 8/15. Find the integers. Thank you.
Answer by aaaaaaaa(138) About Me  (Show Source):
You can put this solution on YOUR website!
reciprocal of x = the number which multiplied by x gives 1.
Therefore, we can express the reciprocal of x as 1%2Fx.
So now, let's assign the variables to the values:
First number = 2x+1
Second number = 2x+3
Reciprocal of first = 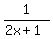1%2F%282x%2B1%29
Reciprocal of second = 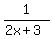1%2F%282x%2B3%29
The assugnment of the two numbers requires ome explanation. As the problem requires the two numbers to be odd, we use a little trick (that 2x is always even), to determine that 2x+1 and 2x+3 will be always odd.
1%2F%282x%2B1%29+%2B+1%2F%282x%2B3%29+=+8%2F15
Take the lcm of the denominators (it's 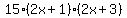15%282x%2B1%29%282x%2B3%29):
15%282x%2B3%29+%2B+15%282x%2B1%29+=+8%282x%2B3%29%282x%2B1%29
30x+%2B+45+%2B+30x+%2B+15+=+32x%5E2+%2B+64x+%2B+24
60x+%2B+60+=+32x%5E2+%2B+64x+%2B+24
32x%5E2+%2B+4x+-+36+=+0
Solved by pluggable solver: SOLVE quadratic equation with variable
Quadratic equation ax%5E2%2Bbx%2Bc=0 (in our case 32x%5E2%2B4x%2B-36+=+0) has the following solutons:

x%5B12%5D+=+%28b%2B-sqrt%28+b%5E2-4ac+%29%29%2F2%5Ca

For these solutions to exist, the discriminant b%5E2-4ac should not be a negative number.

First, we need to compute the discriminant b%5E2-4ac: b%5E2-4ac=%284%29%5E2-4%2A32%2A-36=4624.

Discriminant d=4624 is greater than zero. That means that there are two solutions: +x%5B12%5D+=+%28-4%2B-sqrt%28+4624+%29%29%2F2%5Ca.

x%5B1%5D+=+%28-%284%29%2Bsqrt%28+4624+%29%29%2F2%5C32+=+1
x%5B2%5D+=+%28-%284%29-sqrt%28+4624+%29%29%2F2%5C32+=+-1.125

Quadratic expression 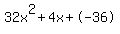32x%5E2%2B4x%2B-36 can be factored:
32x%5E2%2B4x%2B-36+=+32%28x-1%29%2A%28x--1.125%29
Again, the answer is: 1, -1.125. Here's your graph:
graph%28+500%2C+500%2C+-10%2C+10%2C+-20%2C+20%2C+32%2Ax%5E2%2B4%2Ax%2B-36+%29


Since 1.125 is not an integer, x = 1, first = 3 and second = 5.