SOLUTION: sin[cos^-1({{{12/13}}})]. Give as a fraction.

First we look at the inside only:

cos-1()  

That is the answer to this question:

What is the smallest angle in absolute value which has 
for its cosine?

The answer to that question is an angle in the first quadrant.
We don't know right off without a calculator what that angle is.
However we can DRAW IT in standard position, because we know that
the cosine is  or , so we
draw this right triangle in the first quadrant, with the adjacent 
side equal to the numerator of the fraction, x=12, and the hypotenuse
equal to the denominator of the fraction, r=13.  So we draw this:



The angle indicated by the red arc is the angle represented by

cos-1()

[I realize that it takes a while to get used to something that
starts with "COSINE" to represent an ANGLE, but that's what
the little "-1" does. (It's not really a -1, nor is it an exponent,
but unfortunately the mathematicians of old used that notation and 
it stuck, so we are stuck with it, but it is NOT -1 and it is not
an exponent. cos-1 represents an ANGLE which has what follows it as
its cosine.)]

Now let's go back to the original problem:

sin[cos-1()]

We want the SINE of that angle indicated by the red arc and
represented by cos-1().

The sine is 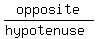, or , so we will 
have to find the opposite side of that angle, which is the y value.

So we call on old man Pythagorus:

 r² = x² + y²
13² = 12² + y²
169 = 144 + y²
 25 = y²
  5 = y

So we get y = 5, so we put that over on the right of the drawing:


 
Now we can find that sine easily as 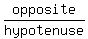 or 
or  

So sin[cos-1()] = 

Edwin