SOLUTION: determine whether quadrilateral MATH is a parallelogram, a rectangle, a rhombus, or a square given the vertices M (5,4), A (3, -6), T ( 0, -10), and H (2,0). Note: I keep comin

Algebra ->  Polygons -> SOLUTION: determine whether quadrilateral MATH is a parallelogram, a rectangle, a rhombus, or a square given the vertices M (5,4), A (3, -6), T ( 0, -10), and H (2,0). Note: I keep comin      Log On


   

Question 554928: determine whether quadrilateral MATH is a parallelogram, a rectangle, a rhombus, or a square given the vertices M (5,4), A (3, -6), T ( 0, -10), and H (2,0). Note: I keep coming up with an answer that doesn't make sense, the other problems, no problem.
Found 2 solutions by Edwin McCravy, KMST:
Answer by Edwin McCravy(20056) About Me  (Show Source):
You can put this solution on YOUR website!
Plot the points and draw the figure MATH:

 M(5,4), A(3,-6), T(0,-10), H(2,0). 



Lines are parallel if they have the same slope.  A parallelogram is
a quadrilateral with both pairs of oposite sides parallel.

So we use the slope formula on all four sides.

m = %28y%5B2%5D-y%5B1%5D%29%2F%28x%5B2%5D-x%5B1%5D%29

Slope of MA:   M (5,4), A (3,-6), 

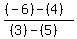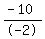m = %28%28-6%29-%284%29%29%2F%28%283%29-%285%29%29 = %28-10%29%2F-2 = 5

Slope of TH:   T(0,-10), and H(2,0). 

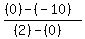m = %28%280%29-%28-10%29%29%2F%28%282%29-%280%29%29 = 10%2F2 = 5

So one pair of sides are parallel since both have slope 5.

Slope of MH:    M(5,4), H(2,0).

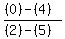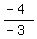m = %28%280%29-%284%29%29%2F%28%282%29-%285%29%29 = %28-4%29%2F%28-3%29 = 4%2F3

Slope of AT:    A(3,-6), T(0,-10),

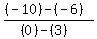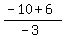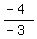m = %28%28-10%29-%28-6%29%29%2F%28%280%29-%283%29%29 = %28-10%2B6%29%2F%28-3%29 = %28-4%29%2F%28-3%29 = 4%2F3
 
So the other pair of sides are also parallel since both have slope 4%2F3.

So MATH is a parallelogram.

Edwin

Answer by KMST(5328) About Me  (Show Source):
You can put this solution on YOUR website!
We can calculate slopes of MA, AT, TH, HM, MT, and AH
For MA, slope = %284-%28-6%29%29%2F%285-3%29=10%2F2=5
For AT, slope = %28-6-%28-10%29%29%2F%283-0%29=4%2F3
For TH, slope = %280-%28-10%29%29%2F%282-0%29=10%2F2=5
For HM, slope = %284-0%29%2F%285-2%29=4%2F3
The fact that opposite sides of quadrilateral MATH have the same slope, means those pairs of opposite sides are parallel. That proves that it is a parallelogram.
If the adjacent sides were perpendicular, we would have four right angles, and it would be a rectangle (or maybe even that special kind of rectangle that we call square). If the sides were perpendicular, the product of their slopes would be -1.
However, %285%29%284%2F3%29=20%2F3 is not -1. So, there are no right angles in MATH. Math is not a square or a rectangle.
Could it be a rhombus? If it were a rhombus, the diagonals would be perpendicular.
Let's calculate the slope of the diagonals
For MT, slope = %284-%28-10%29%29%2F%285-0%29=14%2F5
For AH, slope = %28-6-0%29%2F%283-2%29=-6%2F1=-6
The product of the slopes, -6%2814%2F5%29=-84%2F5 , is not -1, so the diagonals are not perpendicular, and MATH is not a rhombus.
Quadrilateral MATH is a parallelogram. It is neither a square, nor a rectangle, nor a rhombus.