Question 554714: Solve for X i cant remember how to figure it out.
300+900x+900x^2+300x^3=241.5765
Answer by KMST(5328)   (Show Source):
You can put this solution on YOUR website! PS EDIT part 1: I claim temporary insanity. I realized that the solution was laughing at my face after posting my answer. Of course, I was busy, and until now, I could not get back to the computer to correct my embarrassing mistake.
End PS EDIT PART 1.
I do not know that you would get that kind of equation to solve in high school.
It is of degree 3 and has that weird 241.5765 number.
I do not remember a formula to solve cubic equations.
I remember seeing a formula or method once, but it was to painful to even try it.
However, you could get a numerical solution, trying numbers until you get a good approximation.
The graph of
 has a well-known shape.
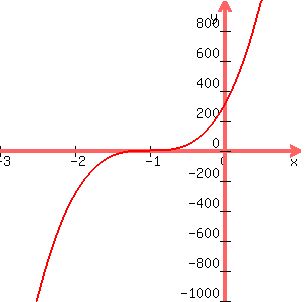
It increases continuously, very steeply for x with large absolute value at both ends, but slows down to a crawl and even seems to stop as it gets to the f(-1)=0, then speeds up again. (Just like me driving past a stop sign).
Your equation is  .
PS EDIT part 2
So  -->  -->  (an exact answer)
The numerical approximation method below is good when the exact answer is not staring at you in the face.
END PS EDIT
We know f(x) increases witth x.
We know f(-1)=0 and can easily see that f(0)=300.
The solution has to be somewhere in between, for some x between -1 and 0.
Without a calculator I can even calculate f(-0.1).
f(-0.1)=300(1-0.300+0.030-0.01)=300(0.729)=218.7
So the solution is between -0.1 and 0.
For more precision, I need a calculator or spreadsheet software.
With tha that I find that -0.06965 is a pretty good approximation.
|
|
|
