Question 554273: I need help solving this problem...looking to find a five digit number:
The 3rd and the 5th digits are equal
1st - 3rd = 2nd - 4th
3rd * 4th = 1st ^ 2 - 1
2nd - 1st = sqrt (5th)
Thank you in advance for your help!
Found 2 solutions by Edwin McCravy, KMST:
Answer by Edwin McCravy(20060)   (Show Source): (Show Source):
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! When faced with a similarly impossible problem that is not answered here, you could give the artofproblemsolving website community a try. The frightfully brainy members of those forums would find an answer if there is one. They used to have a lot of this kind of problem.
MY ANSWER
The two solutions are 11000 and 57464.
THE LONG CASE WORK (Sorry, it's the best I could do).
Let A be the first digit, B the second digit, C the third and fifth digits, and D the fourth digit.
The number would be ABCDC.
We know that A is not zero (or else it would not be a 5 digit number), and that:



The last condition means that C can only be 0, 1, 4, or 9, or else
 would not be an integer. would not be an integer.
It also tells you that  to make to make  , and since , and since
 --> -->  , it also means that , it also means that  and and 
WITH C=0,
 so A=1 so A=1
Also  , so A=B=1 , so A=B=1
Then  turns into turns into  , so D=0. , so D=0.
That would give you the number 11000.
There could be other answers with C=1, C=4, or C=9
 means that the product CD can only be 0, 3, 8, 15, 24, 35, 48, 63, or 80, for A=1, 2, 3, ...9, respectively. However those values have C (1, 4, or 9) as a factor. means that the product CD can only be 0, 3, 8, 15, 24, 35, 48, 63, or 80, for A=1, 2, 3, ...9, respectively. However those values have C (1, 4, or 9) as a factor.
WITH C=1
as a factor, CD=D, and we are limited to 3 of the 9 possibilities above:
CD=D=0 (for A=1), CD=D=3 (for A=2), and CD=D=8 (for A=3).
D=0 does not meet the requirement that 
For the other cases, we can calculate B from  --> --> 
and see if  is true is true
For A=2 and D=3, 
 and and  It does not work. It does not work.
For A=3 and D=8, 
 and and  It does not work. It does not work.
WITH C=4 or C=9
The choices for value of the product CD listed above narrow to
CD=8= (for C=4, A=3) with D=2, (for C=4, A=3) with D=2,
CD=24=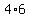 (for C=4, A=5) with D=6, (for C=4, A=5) with D=6,
CD=63=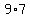 (for C=9, A=8) with D=7 (for C=9, A=8) with D=7
The first choice (C=4, A=3, D=2) and the last one (C=9, A=8, D=7) are eliminated because they do not comply with  . .
For the remaining possibility, we calculate B from  --> --> 
and see if  is true. is true.
For C=4, A=5, D=6 --> 
Then  and and  We have another solution (57464). We have another solution (57464).
|
|
|