SOLUTION: How do you list the possible rational zeros of f in a function using the rational zero theorem? f(x)=x^4+2x^2-24

Algebra ->  Rational-functions -> SOLUTION: How do you list the possible rational zeros of f in a function using the rational zero theorem? f(x)=x^4+2x^2-24      Log On


   

Question 554217: How do you list the possible rational zeros of f in a function using the rational zero theorem?
f(x)=x^4+2x^2-24
Found 2 solutions by richard1234, KMST:
Answer by richard1234(7193) About Me  (Show Source):
You can put this solution on YOUR website!
The possible rational zeros are where p is a factor of the constant term (-24) and q is a factor of the leading coefficient (1). Since q = 1 and we are using plus/minus, the possible rational zeros are simply the positive and negative factors of 24.

Answer by KMST(5328) About Me  (Show Source):
You can put this solution on YOUR website!
POSSIBLE RATIONAL ZEROS
The rational zeros will be rational numbers (fractions) with denominators that are divisors/factors of the leading coefficient, and numerators that are divisors/factors of the independent term.
For f%28x%29=x%5E4%2B2x%5E2-24 the leading coefficient is the invisible 1 in front of x%5E4, and the independent term is -24.
The only positive divisors/factor of 1 is 1.
The positive divisors/factors of 24 are:
1, 2, 3, 4, 6, 8, 12, and 24.
The possible rational zeros are 1, -1, 2, -2, 3, -3, etc.
HOW TO FIND THE POSSIBLE RATIONAL ZEROS
My method to find the factors, was to start with 1, and check integers to see if they would divide 24 evenly. Once I got to a factor that squared was equal or greater than 24, I used another strategy.
Factors come in pairs that multiply to give you 24:
1 x 24 = 24,
2 x 12 = 24
3 x 8 = 24
4 x 6 = 24
Once I got to 6, and saw that 6%5E2=36%3E24,
I found the larger factors from the smaller factors I found before, by dividing as in
24%2F3=8, and 24%2F2=12.
Another method to find the factors is to work form the prime factorization:
24=2%5E3%2A3 so the factors/divisors will all be
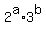2%5Ea%2A3%5Eb, with 0%3C=a%3C=3 and 0%3C=b%3C=1.
There are 4 possible values for a and 2 for b, so I knew there would be 8 factors.
For a number like 24, calculating them as 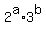2%5Ea%2A3%5Eb would have been a pain, so I used the other method.
NOTE:
To find the zeros of f%28x%29=x%5E4%2B2x%5E2-24, I would solve the equation
x%5E4%2B2x%5E2-24=0 by changing variables to y=x%5E2, so that the equation would transform into
y%5E2%2B2y-24=0 ---> %28y-4%29%28y%2B6%29=0
Back to the original function, I would write it as
f%28x%29=x%5E4%2B2x%5E2-24=%28x%5E2-4%29%28x%5E2%2B6%29=%28x-2%29%28x%2B2%29%28x%5E2%2B6%29
Then I would know that the only real zeros are 2, and -2, which were 2 of the 24 possible rational zeros.
The factor 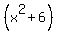%28x%5E2%2B6%29 is not zero for any real value of x.