SOLUTION: If cot<font face = "symbol">q</font> = -3/4 and sin<font face = "symbol">q</font> < 0, then the value of cos<font face = "symbol">q</font> is:

The cotangent, being  is negative, and the cotangent is 
negative in quadrants II and IV

The sine, being < 0, is negative, and the sine is 
negative in quadrants III and IV.

Therefore q is in quadrant IV

The cotangent is  = 

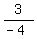So we draw a triangle in quadrant IV with its hypotenuse as
the terminal side of q, its shorter leg x=+3 and its longer leg  
y=-4.  The shorter leg will be taken positive since it goes right,
and the longer leg will be taken negative because it goes down. 
The angle q is indicated by the red arc.

 

Now we calculate r, the hypotenuse, by the Pythagorean theorem:

r² = x² + y²
r² = (3)² + (-4)²
r² = 9 + 16
r² = 25
 r = 5

 

Now since we want cos(q), we know that cos(q) =  = .
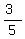It is positive as we would expect an angle's cosine to be in quadrant IV.

Edwin