SOLUTION: The question is: Show that {{{(2x+1)}}} is a factor of the polynomial {{{ 2x^3+5x^2+8x+3}}}. Hence express {{{(2x^4+5x^3+11x^2-15x-3)/(2x^3+5x^2+8x+3)}}} into partial fra

Algebra ->  Polynomials-and-rational-expressions -> SOLUTION: The question is: Show that {{{(2x+1)}}} is a factor of the polynomial {{{ 2x^3+5x^2+8x+3}}}. Hence express {{{(2x^4+5x^3+11x^2-15x-3)/(2x^3+5x^2+8x+3)}}} into partial fra      Log On


   

Question 552497: The question is:
Show that %282x%2B1%29 is a factor of the polynomial +2x%5E3%2B5x%5E2%2B8x%2B3. Hence express
%282x%5E4%2B5x%5E3%2B11x%5E2-15x-3%29%2F%282x%5E3%2B5x%5E2%2B8x%2B3%29
into partial fractions.
I know how to show that 2x+1 is a factor of the polynomial.. I don't know how to express that into partial fractions.
Thank You.
Answer by AnlytcPhil(1806) About Me  (Show Source):
You can put this solution on YOUR website!
%282x%5E4%2B5x%5E3%2B11x%5E2-15x-3%29%2F%282x%5E3%2B5x%5E2%2B8x%2B3%29


Since the numerator has a higher degree than the denominator, before we can do
partial fractions, we must first do the long division to get a rational
expression which has a numerator of lower degree than the denominator:

                                        x + 0                                
2x³ + 5x² + 8x + 3)2x4 + 5x³ + 11x² - 15x - 3
                   2x4 + 5x³ +  8x² +  3x
                         0x³ +  3x² - 18x - 3
                         0x³ +  0x² +  0x + 0
                                3x² - 18x - 3

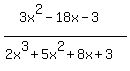%282x%5E4%2B5x%5E3%2B11x%5E2-15x-3%29%2F%282x%5E3%2B5x%5E2%2B8x%2B3%29 = x + %283x%5E2-18x-3%29%2F%282x%5E3%2B5x%5E2%2B8x%2B3%29

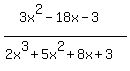We'll break %283x%5E2-18x-3%29%2F%282x%5E3%2B5x%5E2%2B8x%2B3%29 into partial fractions.  Then
we'll come back and add the x quotient to it.

Now we factor the denominator.  We are told that 2x+1 is a factor, so we
divide that into the denominator

              x² + 2x + 3      
2x + 1)2x³ + 5x² + 8x + 3
       2x³ +  x²
             4x² + 8x
             4x² + 2x
                   6x + 3
                   6x + 3 

x²+2x+3 does not factor, so we have 

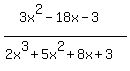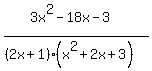%283x%5E2-18x-3%29%2F%282x%5E3%2B5x%5E2%2B8x%2B3%29 = %283x%5E2-18x-3%29%2F%28%282x%2B1%29%28x%5E2%2B2x%2B3%29%29

to break into partial fractions:


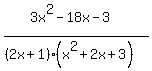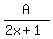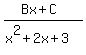%283x%5E2-18x-3%29%2F%28%282x%2B1%29%28x%5E2%2B2x%2B3%29%29 = A%2F%282x%2B1%29 + %28Bx%2BC%29%2F%28x%5E2%2B2x%2B3%29

Multiply through by the LCD

3x² - 18x - 3 = A(x² + 2x + 3) + (Bx + C)(2x + 1)

This must be true for all values of x, so we substitute various values for x:

Substituting x=0

3(0)² - 18(0) - 3 = A((0)² + 2(0) + 3) + (B(0) + C)(2(0) + 1)

               -3 = 3A + C 

Substituting x=1

3(1)² - 18(1) - 3 = A((1)² + 2(1) + 3) + (B(1) + C)(2(1) + 1)
       3 - 18 - 3 = A(1 + 2 + 3) + (B + C)(2 + 1)
              -18 = A(6) + (B + C)(3)
              -18 = 6A + 3B + 3C

Substituting x=-1

3(-1)² - 18(-1) - 3 = A((-1)² + 2(-1) + 3) + (B(-1) + C)(2(-1) + 1)
       3 + 18 - 3 = A(1 - 2 + 3) + (-B + C)(-2 + 1)
               18 = A(2) + (-B + C)(-1)
               18 = 2A + B - C

So we solve the system of three equations:

-3 = 3A + C
-18 = 6A + 3B + 3C
18 = 2A + B - C

and get A=3, B=0, C=-12

So

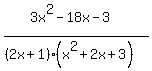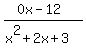
%283x%5E2-18x-3%29%2F%28%282x%2B1%29%28x%5E2%2B2x%2B3%29%29 = 3%2F%282x%2B1%29 + %280x-12%29%2F%28x%5E2%2B2x%2B3%29
 
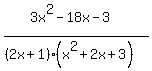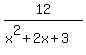 %283x%5E2-18x-3%29%2F%28%282x%2B1%29%28x%5E2%2B2x%2B3%29%29 = 3%2F%282x%2B1%29 - 12%2F%28x%5E2%2B2x%2B3%29

Therefore going back to the original problem:

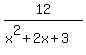%282x%5E4%2B5x%5E3%2B11x%5E2-15x-3%29%2F%282x%5E3%2B5x%5E2%2B8x%2B3%29 = x + 3%2F%282x%2B1%29 - 12%2F%28x%5E2%2B2x%2B3%29

Edwin