SOLUTION: My teacher did not explain any of this stuff to us, so if someone could please EXPLAIN both these types of problums to me that would be awesome. 1) log 7 = 0.8 log 12 = 1.1

logB(A) asks the question:

To what exponent must the base B be raised to give A?  
That exponent is the answer to what logB(A) equals. 

Because logarithms are exponents, and because we can 
add exponents of a base in order to multiply, subtract them in 
order to divide, and multiply them to raise a power to a power, 
we have these three corresponding rules for logarithms:

1.  logB(A·C) = logB(A) + logB(C)
2.  logB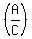 = logB(A) - logB(C)
3.  logB(AC) = C·logB(A)

[If the base B isn't written, it's understood to be 10.]
 
--------------------------------------

1) log(7) = 0.8
log(12) = 1.1
log(8)= 0.9
Find log

Use rule 2:

2.  logB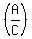 = logB(A) - logB(C)

with A=1, B=64, and the base B understood as 10

    log = log(1) - log(64)

Now we use the definition of logarithms to find log(1).
We ask the question "To what power must the base 10 be raised to get 1?"
If you remember that 100 = 1, then you know that log(1)
is 0.  In fact the logarithm of 1 is always 0, regardless of the base.  
So now we have

    log = 0 - log(64)
or
     -log(64)

We are given the values of these three logs with understood base 10: 
 log(7) = 0.8, log(12) = 1.1, log(8)= 0.9

Now we ask:  Which of these numbers 7, 12, or 8, can we multiply
together, divide, or raise to a power, to get 64?
The answer: we can get 64 by squaring 8. That is, 8² = 64.

So we replace 64 by 8² and now we have:

     -log(8²)

Now we use rule 3:

3.  logB(AC) = C·logBA
with A=8 and C=2

and we have:

   -log(82) = -2·log(8)

And since we are given log(8) = 0.9

   -2·log(8)
   -2·(0.9)
     -1.8 

That's the answer, -1.8.  Try hard to follow the above.

--------------------------------------------


2)log5(11) = 1.5
log5(6) = 1.1
log5(4) = 0.9
Find log5(264)

We are given the values of these three logs with base 5: 
log5(11) = 1.5, log5(6) = 1.1, log5(4) = 0.9

Now we ask:  Which of these numbers 11, 6, and 4, can we multiply
together, divide, or raise to a power, to get 264?

To answer that we must see if 264 can be divided evenly by one of those.
We find the 264÷11 = 24. So we write 
264 = = 11·24 and we write

   log5(264) = 
   log5(11·24)

Now we use rule 1:

1.  logB(A·C) = logB(A) + logB(C)
with A=11, B=5, C=24

    log5(11·24) = log5(11) + log5(24)

We substitute the given log5(11) = 1.5, and we have:

    1.5 + log5(24)

Now we ask:  Which of these numbers 11, 6, and 4, can we multiply
together, divide, or raise to a power, to get 24?  That answer is easy.
24 = 6·4.  So we replace 24 by 6·4, and we have:

    1.5 + log5(6·4)

Now we use rule 1 again:

1.  logB(A·C) = logB(A) + logB(C)
this time with with A=6, B=5, C=4


    1.5 + log5(6) + log5(4)
   
and we are give those logs, so we substitute:

    1.5 + 1.1 + 0.9

Answer: 3.5

---------------------------------------
Edwin