SOLUTION: Solve the equations: 4log4x - 3log5y =1 log2x - log5y =2

I can't tell which of these you meant:

4log(4x) - 3log(5y) = 1     or   4log4(x) - 3log5(y) = 1
 log(2x) -  log(5y) = 2           log2(x) -  log5(y) = 2

I tried doing it the first way and there was no solution, 
so I think you must have meant the second way.  

4log4(x) - 3log5(y) = 1
 log2(x) -  log5(y) = 2

I will change the first term in the first equation so 
it will be a log to the base 2, like the first term in
the second equation.  Using the change of base formula 
on that term:

4log4(x) = 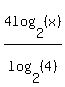 =  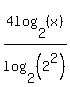=  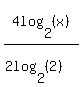=  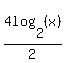= 2log2(x) 

The system of equations is now:

2log2(x) - 3log5(y) = 1
 log2(x) -  log5(y) = 2

let u = log2(x) 
let v = log5(y)

The system of equations is now:

2u - 3v = 1
 u -  v = 2

Solve that system of equations by substitution or elimination
and get (u,v) = (5,3).  I'm sure you can do that.

But we don't want u and v, we want x and y.
So we substitute back:

u = log2(x), which is equivalent to the exponential equation:

x = 2u = 25 = 32

v = log5(y)

y = 5v = 53 = 125

So the solution is

(x,y) = (32,125)

Edwin