Question 552037: I am told to use my trigonometric tables and then find (a) find sin 26.1 degrees
and then (b) find the acute angle, 0, to the nearest tenth of a degree if cos0=.8084.
-These 0 are strange 0's with a line in the middle of the zero.
If someone could please help me with this and explain fully, I'm so confused in this area of Algebra I'm learning.
Thanks a lot!
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! Angles are often represented with Greek letters.
The Greek letter theta looks like this  . .
Half a century ago, we used to look up values for sine and cosine in trigonometric tables. (We also looked up logarithms in tables. There were no calculators back then). I have not looked at a trigonometric table for a long time. Your table may be different from the ones I have seen. The one I used back then would have angle measurements in degrees on a column on the left, with (additional) fractions of a degree as headings on a line at the top. On the right hand side we had a column with the measure of the complementary angle in degrees (with additional fractions on a line at the bottom. The numbers in the middle of the table were sine of the angle read at left and cosine of the supplementary angle read at right.
I could not find my old table, but I have an abbreviated one. It tells me that
(a) 
(b) It also says that 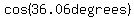 is about 0.8084. is about 0.8084.
So if  , ,  (to the nearest tenth of a degree). Because trigonometric functions are periodic, and (to the nearest tenth of a degree). Because trigonometric functions are periodic, and  , there are infinity of other angles with the same cosine, like -36.1 degrees, (-36.1+360) degrees, (-36.1+720) degrees, and so on, as well as (36.1+360) degrees, (36.1+720) degrees, and so on. However, the only acute angle , there are infinity of other angles with the same cosine, like -36.1 degrees, (-36.1+360) degrees, (-36.1+720) degrees, and so on, as well as (36.1+360) degrees, (36.1+720) degrees, and so on. However, the only acute angle  with with  is 36.1 degrees. is 36.1 degrees.
|
|
|