SOLUTION: find the sum of the series using this symbol for the following problems: ------> Ʃ please show your work because i don't know how to do these. Also on 51 the answer is 1

Algebra ->  Decimal-numbers -> SOLUTION: find the sum of the series using this symbol for the following problems: ------> Ʃ please show your work because i don't know how to do these. Also on 51 the answer is 1      Log On


   

Question 551086: find the sum of the series
using this symbol for the following problems: ------> Ʃ
please show your work because i don't know how to do these. Also on 51 the answer is 1110 but how? so work on each of the problems would be very liked.
thank you for ur help and happy new year!
51. 20 on top of symbol, i=1 on bottom,(3+5i) on right
52. 34 on top, i=1 on bottom,(1+8i) on right
53. 15 on top, i=1 on bottom, (-10-3i) on right
54. 22 on top, i=1 on bottom, (6-3/4i) on right
55. 45 on top, i=1 on bottom, (11+4i) on right
56. 18 on top, i=1 on bottom, (8.1+4.4i) on right
Found 2 solutions by Edwin McCravy, KMST:
Answer by Edwin McCravy(20060) About Me  (Show Source):
You can put this solution on YOUR website!
The trick is to use the distributive principle.  Then use the 
special formulas:

1. You can distribute ∑ over a sum or difference of terms.
2. You can take out a constant in front of the ∑.

I'll just do this one and you can easily do the rest.

51. 20 on top of symbol, i=1 on bottom,(3+5i) on right.

sum%28%283%2B5%2Ai%29%2Ci=1%2C20%29

First distribute the ∑ over the sum like this:

sum%28%283%29%2Ci=1%2C20%29 + sum%28%285%2Ai%29%2Ci=1%2C20%29

Write the 3 as 3·1

sum%28%283%2A1%29%2Ci=1%2C20%29 + sum%28%285%2Ai%29%2Ci=1%2C20%29

Now you can take the constant 3 out in front of the first 
summation and take the constant 5 out in front of the second
summation, like this:

3%2Asum%28%281%29%2Ci=1%2C20%29 + 5%2Asum%28%28i%29%2Ci=1%2C20%29

Now you can use the special formulas:

3%2A20 + 5%2Aexpr%28%28%2820%29%2820%2B1%29%29%2F2%29 = 60 + 5%2Aexpr%28%28%2820%29%2821%29%29%2F2%29 = 60 + 1050 = 1110.

Now you can do all of them by using the distributive principle first
and then using the special formulas.

Edwin

Answer by KMST(5328) About Me  (Show Source):
You can put this solution on YOUR website!
All of your problems are sums of arithmetic sequences.
My problem is that I do not know what strategy you were expected to use to solve them. My way of solving them may not be what your teacher expects. You may be expected to look up a formula in your textbook and apply it, and the calculation may be different from the one I would do (same result, of course).
Your textbook or class notes may tell you that an arithmetic sequence can be represented as
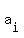a%5B1%5D, a%5B2%5D, a%5B3%5D, .... a%5Bi%5D, ...
with a%5Bi%5D=a%5B0%5D%2Bid
with the values of 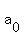a%5B0%5D and d determining the sequence.
Then they could have said that
.
The way your problems read, you are given 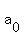a%5B0%5D, n, and d, so that formula will work well.
Another formula you could have been given is
sum%28+a%5Bi%5D%2C+i=1%2C+n+%29=n%2A%28a%5B1%5D%2Ba%5Bn%5D%29%2F2
That one is the easiest to derive for me (I don't memorize formulas; I just derive them from the definitions as needed). It would be easiest to use if you had the first and last terms already calculated.
You may have been given some other equivalent expression.
My best guess is that you are expected to use the first formula above, so I'll go with that.
51. sum%28+%283%2B5i%29%2C+i=1%2C+20+%29=20%2A3%2B20%2A21%2A5%2F2=60%2B1050=1110
(You could also say a%5B1%5D=3%2B5=8, and a%5B20%5D=3%2B5%2A20=3%2B100=103, so
sum%28+a%5Bi%5D%2C+i=1%2C+20+%29=20%2A%288%2B103%29%2F2=20%2A111%2F2=1110, using the second formula).
52. sum%28+%281%2B8i%29%2C+i=1%2C+34+%29=34%2A1%2B34%2A35%2A8%2F2=34%2B4760=4794
53. sum%28+%28-10-3i%29%2C+i=1%2C+15+%29=15%2A%28-10%29%2B15%2A16%2A%28-3%29%2F2=-150-360=-510
54.
55. sum%28+%2811%2B4i%29%2C+i=1%2C+45+%29=45%2A11%2B45%2A46%2A4%2F2=495%2B4140=4635
56. sum%28+%288.1%2B4.4i%29%2C+i=1%2C+18+%29=18%2A8.1%2B18%2A19%2A4.4%2F2=145.8%2B752.4=898.2
Because I do not memorize formulas, I would have calculated it like this:
, splitting the sum into other sums, to make it easier to use the formula that makes more sense to me, but I bet that's not what your teacher expects.