|
Question 551085: for part (a) find the sum of the first n terms of the arithmetic series. for part (b) find n for the given sum Sn.
45. 3+8+13+18+23+...
a. n=20
b. Sn=366
46. 50+42+34+26+18+...
a. n=40
b. Sn=182
47. -10+(-5)+0+5+10+...
a. n=19
b. Sn=375
48. 34+31+28+25+22+...
a. n=32
b. Sn=-12
49. 2+9+16+23+30+...
a. n=68
b. Sn=1661
50. 2+16+30+44+58+...
a. n=24
b. Sn=2178
please show your work also so i know how to do it,
thank you for ur help and happy new year!
Found 2 solutions by mathstutor458, KMST:
Answer by mathstutor458(57)   (Show Source):
You can put this solution on YOUR website! 45. 3+8+13+18+23+... is arithmatic sequence
first term a1= 3, difference d=8-3=5
a. n=20
The sum of the first n terms of the arithmetic series Sn=(n/2)(2a1+(n-1)d)
the sum of the first 20 terms of the arithmetic series=(20/2)(2*3 + (20-1)*5)
=10*(6+19*5)=10*(6+95)
=10*101=1010 ----->answer
b. Sn=366
The sum of the first n terms of the arithmetic series Sn=(n/2)(2a1+(n-1)d)
(n/2)(2a1+(n-1)d)=366
n(2*3+(n-1)5)=366*2
6n+5n^2-5n=732
5n^2+n-732=0
5n^2-60n+61n-732=0
5n(n-12)+61(n-12)=0
(5n+61)(n-12)=0
Therefore, n=12 positive number,we dont consider fractional numbers.
n=12--------> answer
46. 50+42+34+26+18+...is arithmatic sequence
first term a1= 50, difference d=42-50=-8
a. n=40
The sum of the first n terms of the arithmetic series Sn=(n/2)(2a1+(n-1)d)
the sum of the first 40 terms of the arithmetic series=(40/2)(2*50 + (40-1)(-8))
=20*(100+39(-8))
=20*(100-312)
=20*(-212)=-4240 -------> is sum of 40 numbers(answer)
b. Sn=182
The sum of the first n terms of the arithmetic series Sn=(n/2)(2a1+(n-1)d)
(n/2)(2a1+(n-1)d)=182
n(2*50+(n-1)(-8))=182*2
n(100-8n+8)=364
-8n^2+108n-364=0
-8n^2+56n+52n-364=0
-8n(n-7)+52(n-7)=0
(n-7)(-8n+52)=0
n=7 positive number,we dont consider fractional numbers.
n=7--------> answer
47. -10+(-5)+0+5+10+...is arithmatic sequence
first term a1= -10, difference d=-5-(-10)=-5+10=5
a. n=19
The sum of the first n terms of the arithmetic series Sn=(n/2)(2a1+(n-1)d)
the sum of the first 19 terms of the arithmetic series=(19/2)(2*(-10)+(19-1)5)
=(19/2)(-20+18*5)=(19/2)(-20+80)
=(19/2)60=19*30=570-------> is sum of 19 numbers(answer)
b. Sn=375
The sum of the first n terms of the arithmetic series Sn=(n/2)(2a1+(n-1)d)
(n/2)(2a1+(n-1)d)=375
(n/2)(2*(-10) + (n-1)(5)) = 375
(n)(-20+5n-5)=375*2
5n^2-25n=750
5n^2-25n-750=0
5n^2-75n+50n-750=0
5n(n-15)+50(n-15)=0
(n-15)(5n+50)=0
n=15 positive number,we dont consider fractional numbers.
n=15--------> answer
48. 34+31+28+25+22+...is arithmatic sequence
first term a1= 34, difference d=31-(34)=-3
a. n=32
Sn=(n/2)(2a1+(n-1)d)
S32=(32/2)(2*34+(32-1)(-3))=16*(68-93)=-400
b. Sn=-12
Sn=(n/2)(2a1+(n-1)d)
(n)(2*34+(n-1)(-3))=-12*2
68n-3n^2+3n+24=0
-3n^2+71n+24=0
(n-24)(-3n-1)=0
n=24 positive number,we dont consider fractional numbers.
n=24--------> answer
49. 2+9+16+23+30+...
first term a1= 2, difference d=9-2=7
a. n=68
Sn=(n/2)(2a1+(n-1)d)
S68=(68/2)(2*2+(68-1)7)
=34*(4+469)=16082
b. Sn=1661
Sn=(n/2)(2a1+(n-1)d)
(n)(2*2+(n-1)7)=1661*2
4n+7n^2-7n-3322=0
7n^2-3n-3322=0
(n-22)(7n+151)=0
n=22 positive number,we dont consider fractional numbers.
n=22--------> answer
50. 2+16+30+44+58+...
first term a1= 2, difference d=16-2=14
a. n=24
Sn=(n/2)(2a1+(n-1)d)
S24=(24/2)(2*2+(24-1)14)
=12(4+322)=12*326=3912
b. Sn=2178
Sn=(n/2)(2a1+(n-1)d)
(n)(2*2+(n-1)14)=2178*2
4n+14n^2-14n-4356=0
14n^2-10n-4356=0
(n-18)(14n+242)=0
n=18 positive number,we dont consider fractional numbers.
n=18--------> answer
Answer by KMST(5328)  (Show Source):
You can put this solution on YOUR website! My best guess is that your textbook or class notes tell you that the nth term of an arithmetic sequence,  , can be calculated based on the first term,  , and the common difference,  , as
 .
Then they must have told you that the sum of the first n terms can be calculated as
 or
SOLUTIONS FOR THE FIRST TWO PROBLEMS
45. 3+8+13+18+23+...
 and the common difference is
a. n=20 Since you are not given  , use the second formula
b. Sn=366 I don't think I ever did this kind of problem.
I suppose they could expect you to use a guess and check strategy, and you could try n=10, and figure out that the answer is between 10 and 20.
Otherwise, it gets complicated, but here it goes:
With plus  for this sequence, it means
 , and multiplying both sides times 2
 -->  -->  --> 
Applying the quadratic formula:
That gives us  , our answer.
We disregard the other solution because it's negative, and we were looking for a positive integer for  .
46. 50+42+34+26+18+...
has  and  .
That means  , and  , with all the terms after that being negative.
What's more the sum of the positive terms (the first 7 terms) is
 , which answers part b by lucky guess.
a. n=40
b. Sn=182 We answered it by guess above, but if we need to solve quadratic equations again:
, so 
So,  --> -->  -->  --> 
If you are good at factoring you see that  to find the solutions to the equation. Otherwise, you apply the quadratic formula. Either way, you find the answer to part b  ,
and another solution to the equation, 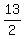 , that we discard because it's not a positive integer.
FOR THE REST
I hope you know how to do it now. I also hope that guess and check is an accepted and viable alternative to find the answer to part b.
Here are the answers I calculated for problems 47-50
47. -10+(-5)+0+5+10+...
a. n=19 
b. Sn=375  
48. 34+31+28+25+22+...
a. n=32 
b. Sn=-12  
49. 2+9+16+23+30+...
a. n=68 
b. Sn=1661  
50. 2+16+30+44+58+...
a. n=24 
b. Sn=2178  
|
|
|
| |
