Question 551083: If a stone is tossed from the top of a 210 meter building, the height of the stone as a function of time is given by h(t) = -9.8t2 – 10t + 210, where t is in seconds, and height is in meters. After how many seconds will the stone hit the ground? Round to the nearest hundredth’s place; include units in your answer.
I got
-10(9.8t^2 - 10t + 210)=0
98t + 100t - 2100
49t^2 + 50t - 1050
t= 4.15 seconds
Am I close??
Answer by Alan3354(69443)   (Show Source): (Show Source):
You can put this solution on YOUR website! If a stone is tossed from the top of a 210 meter building, the height of the stone as a function of time is given by h(t) = -9.8t2 – 10t + 210, where t is in seconds, and height is in meters. After how many seconds will the stone hit the ground? Round to the nearest hundredth’s place; include units in your answer.
I got
-10(9.8t^2 - 10t + 210)=0
98t + 100t - 2100
49t^2 + 50t - 1050
t= 4.15 seconds
Am I close??
--------------------
| Solved by pluggable solver: SOLVE quadratic equation (work shown, graph etc) |
Quadratic equation  (in our case (in our case  ) has the following solutons: ) has the following solutons:

For these solutions to exist, the discriminant  should not be a negative number. should not be a negative number.
First, we need to compute the discriminant  : :  . .
Discriminant d=8332 is greater than zero. That means that there are two solutions:  . .


Quadratic expression 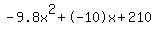 can be factored: can be factored:

Again, the answer is: -5.16733620703838, 4.14692804377307.
Here's your graph:
 |
4.15 is the correct solution, but
------
On Earth, it's h(t) = -4.9t2 – 10t + 210, not -9.8t^2
The -10t indicates it was thrown at 10 m/sec downward.
--------
I got
-10(9.8t^2 - 10t + 210)=0
98t + 100t - 2100 **** you dropped the = 0 here
49t^2 + 50t - 1050
--------
Where did you get the equation with the -9.8t^2 ?
|
|
|