Question 550973: A town is organizing a parade. There will be 2 float sizes. One is 30ft and the other is 15ft. A 10 ft space will be left after each float.
A.The parade must be a least 150ft long, but less than 200ft long. What combinations of large and small floats are possible?
B. Large float costs $600 to operate. Small floats cost $300 to operate. The town has a budget of $2500 to operate the floats. How does this change your answers to part A? What combinations of large and small floats are possible?
Answer by Theo(13342)   (Show Source): (Show Source):
You can put this solution on YOUR website! your cost equation is:
c = 600x + 300y
your cost has to be less than or equal to 2500, so your cost constraint becomes:
600x + 300y <= 2500
anything that costs over 2500 is rejected.
x = number of large floats
y = number of small floats
the formula for the maximum number of large floats is:
40x - 10 <= 200
this becomes 40x <= 210 which becomes:
x <= 210/40
this means that x has to be <= 5.25 which means that x has to be <= 5 since x has to be an integer.
the formula for the maximum number of small floats is:
25y - 10 <= 200
this becomes 25x <= 210 which becomes:
y <= 210/25
this means that y has to be <= 8.4 which means that y has to be <= 8 since y has to be an integer.
so far the constraints are:
x <= 5
y <= 8
the formula for the minimum number of floats in the parade is:
40x + 25y - 10 >= 150
add 10 to each side of this equation to get:
40x + 25y >= 160
the formula for the maximum number of floats in the parade is:
40x + 25y - 10 <= 200
add 10 to each side of this equation to get:
40x + 25y <= 210
the cost equation for this problem is:
600x + 300y <= 2500
this equation is both a constraint and the objective function of this problem.
we want the minimum cost and the cost has to be less than or equal to 2500.
we solve this equation graphically by doing the following:
graph the equation of y = 8
graph the equation of x = 5
graph the equation of 40x + 25y <= 210
graph the equation of 40x + 25y >= 160
graph the equation of 600x + 300y <= 2500
your graph will look something like the following:

your area of compatibility will be below the graph of 600x + 300y = 2500 and above the graph of 40x + 25y = 160.
that area is shown in the following diagram.
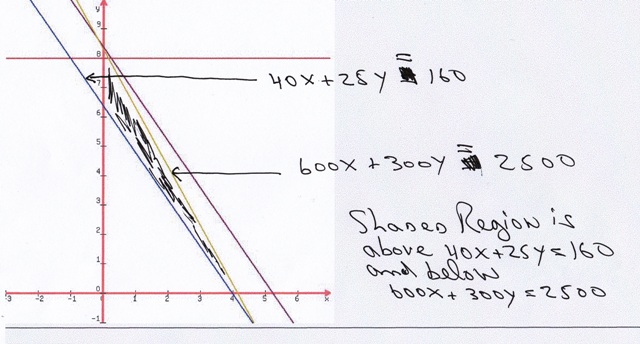
it is within this region that all constraints are met.
all combinations within that region will have a parade length greater than or equal to 150 feet and less than or equal to 200 feet and will come within the maximum cost of 2500.
based on the properties of linear programming, the minimum / maximum points of the objective function are at the corners of the compatible region.
in this graph, those corners would be (x,y) coordinate points of:
(4,0)
(0,7)
(0,8)
while (7,0) and (8,0) are technically not at the corners, they are the nearest integers to those corners and one of the requirements are that x and y are integers.
when x = 4, the number of floats in the parade are 4 large and 0 small and the total cost is 600 * 4 = 2400 which is under the limit and the total number of feet required is 4*40 - 10 = 150 which is within the limits of 150 t 200 feet.
when y = 7, the number of floats in the parade are 0 large and 7 small and the total cost is 300 * 7 = 2100 which is under the limit and the total number of feet required is 7*25 - 10 = 165 which is within the limits of 150 to 200 feet.
when y = 8, the number of floats in the parade are 0 large and 8 small and the total cost is 300 * 8 = 2400 which is under the limit and the total number of feet required is 8* 25 - 10 = 190 feet which is within the limits of 150 to 200 feet.
the minimum cost combination is 0 large floats and 7 small floats.
there are other possible combinations that will be within the compatibility region.
those possible combinations are shown in the following table:
large floats small floats feet required cost
0 7 165 2100
0 8 190 2400
1 5 155 2100
1 6 180 2400
2 4 170 2400
3 2 160 2400
4 0 150 2400
the minimum cost is at (0,7).
it is also at (1,5).
this stands to reason since 1*600 = 2*300 so you can exchange 1 large float for 2 small floats from a cost perspective and break even.
the fact that (1,5) is also a minimal cost does not negate the fact that the minimum or maximum value will be at the corners.
it still is, even though a value not at a corner is also a minimal cost.
|
|
|