|
Question 550844: The points A(-1,2),B(x,y) and C=(4,5) are such that BA=BC.Find a linear relation between x and y.
Found 2 solutions by Theo, ikleyn:
Answer by Theo(13342)   (Show Source): (Show Source):
You can put this solution on YOUR website! point B will be any point on the perpendicular bisector of AC.
as such it will be equidistant between A and C which will always make AB = BC.
the linear relationship is the equation of the line that passes through the midpoint of AC and is perpendicular to it.
the equation of the line AC is:
y = (3/5)x + (13/5)
the equation of the line perpendicular to AC and passing through its midpoint is:
y = -(5/3)x + 6
the graph of the equations for those line is shown below:

point B is any point on the line perpendicular to AC, so the linear relationship between the x value of that point and the y value of that point is the equation of the line perpendicular to AC which is the equation:
y = -(5/3)x + 6.
a picture of the relationship is shown below:
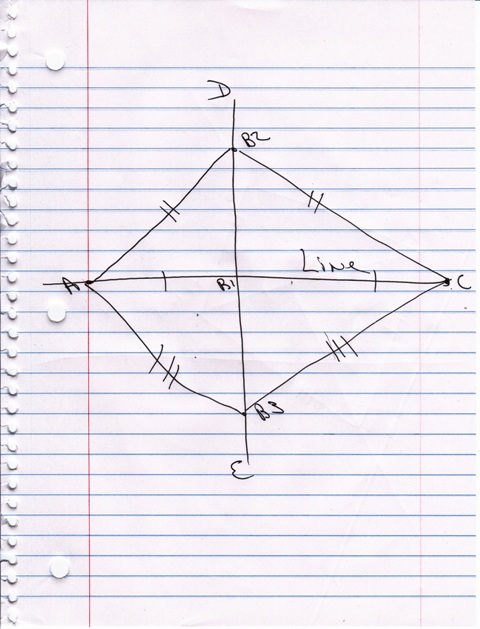
line DE is perpendiculat to line AC.
any point on line DE is equidistant from A and C.
Answer by ikleyn(52835)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
The points A(-1,2), B(x,y) and C(4,5) are such that BA=BC. Find a linear relation between x and y.
~~~~~~~~~~~~~~~~~~~~~~~~~
This problem has a nice Algebra solution.
The square of the length of AB is
|AB|^2 = (x-(-1))^2 + (y-2)^2 = (x+1)^2 + (y-2)^2 = x^2 + 2x + 1 + y^2 - 4y + 4 = x^2 + 2x + y^2 - 4y + 5.
The square of the length of BC is
|BC|^2 = (x-4)^2 + (y-5)^2 = x^2 - 8x + 16 + y^2 - 10y + 25 = x^2 - 8x + y^2 - 10y + 41.
The condition |BA| = |BC| is the same as |AB|^2 = |BC|^2. It gives this equation
x^2 + 2x + y^2 - 4y + 5 = x^2 - 8x + y^2 - 10y + 41.
Combine like terms. The final equation is
10x + 6y = 36,
or
5x + 3y = 18,
or
y = 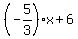 . <<<---=== ANSWER . <<<---=== ANSWER
Solved.
|
|
|
| |