The smallest two angles in every triangle are acute angles (have measure
less than 90°). Sometimes the largest angle is also acute (has measure less
than 90°), sometimes it is right (has measure exactly 90°). and sometimes it is
obtuse (has measure greater than 90°).
If the largest angle is also an acute angle, the triangle is said to be "an acute triangle".
If the largest angle is a right angle, the triangle is said to be "a right
triangle".
If the largest angle is an obtuse angle, the triangle is said to be "an obtuse
triangle".
The triangle yoiu are talking about is isosceles with a base angle of 40°.
So we draw it:
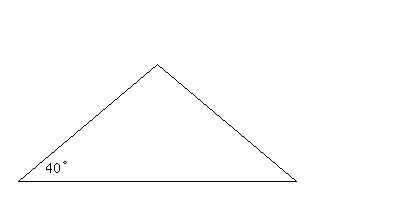Now since it is isosceles, we know that the other base angle is also 40°.
So we label it 40° also
They are both acute angles since 40° is less than 90°. So we need to
know about the largest angle, which is the vertex angle of the isosceles
triangle. We can look and see that it looks like it's obtuse, but in
geometry, we can't go by "what it looks like is true". We have to prove it.
Let's suppose the vertex angle is x°.
Since we know the three interior angles of every triangle totals 180°, we
have:
x° + 40° + 40° = 180°
We combine the terms 40° and 40° and get 80°
x° + 80° = 180°
We subtract 80° from both sides and get
x° = 100°
Since 100° is more than 90° the largest angle is obtuse, and so the
triangle is an obtuse triangle.
Edwin
