SOLUTION: Find the number of integers less than 2011 that has only 3 factors.

Theorem:
A positive integer has exactly three factors if and only if it is
the square of a prime number.

If p is a prime number then p² has exactly three factors 1, p, and p².

Assume for contradiction that n is not the square of a prime but has 
exactly 3 factors.  If it is the square of a composite integer then it
has more than 3 factors, and we have a contradiction.  So n is not a
perfect square.  Let k be the third factor other than 1 and n.   
Then 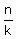 is also a factor, and  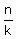is not equal to k
since n is not a perfect square.  So n has more than 3 factors, and
a contradiction is reached.

So we must find the largest square of a prime that does not exceed 2011.

Its prime square root must not exceed the square root of 2011 which is
44.84417465

So the primes less than that are

2,3,5,7,11,13,17,19,23,29,31,37,41,43

There are 14 of them and all their squares are the only integers less
than 2011 which have exactly 3 factors.

Answer 14

Edwin