|
Question 550139: a sphere is placed in an inverted hollow conical vessel of base radius 5cm and vertical height 12cm.If the highest point of the sphere is at the level of the base of the cone,find the radius of the sphere.this is the question for which i'm breaking my head.pls...anybody help me.
Answer by Theo(13342)   (Show Source): (Show Source):
You can put this solution on YOUR website! if you take a cross section of the sphere and the cone and turn it upside down, you will get an isosceles triangle that is circumscribing a circle as shown in the following diagram:
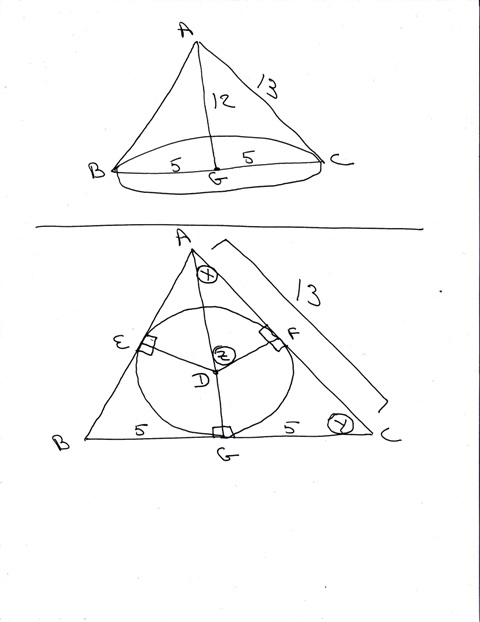
the altitude to the cone is also the altitude of this isosceles triangle.
this forms 2 right triangles.
they are triangle ABC and AGC.
we'll work with right triangle AGC.
the altitude of this right triangle is AG which is equal to 12.
the other leg of this right triangle is GC which is equal to 5.
the hypotenuse of right triangle AGC is AC.
the length of AC is found using the pythagorean formula of a^2 + b^2 = c^2
in right triangle AGC, AG is equal to a which is equal to 12 and CG is equal to b which is equal to 5.
c^2 is therefore equal to 12^2 + 5^2 which is equal to 169 which makes c = to square root of 169 which is equal to 13.
the tangent of angle x is equal to opposite / adjacent which is equal to GC / AG which is equal to 5/12.
this makes angle x equal to 22.61986495 degrees.
ED, FD, and GD are radii of the circumscribed circles and of the circumscribed sphere.
this makes them equal to each other.
they are also apothems of cicumscribing cone and isosceles triangle.
as apothems, they form right angles with the sides of the circumscribing isosceles triangle.
we have 2 right triangles formed that are similar to each other.
they are triangles AGC and AFD.
both angle z and angle y are complementary to angle x which makes them equal to each other.
the triangles formed have all angles equal to each other and are therefore similar to each other.
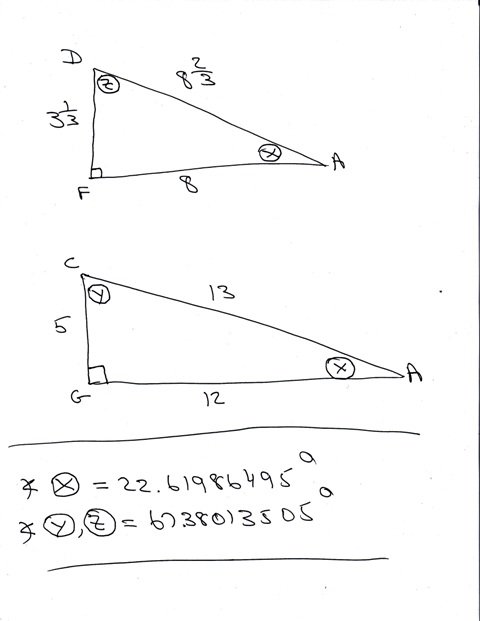
the corresponding side of each triangle that are porportional to each other would be:
AC and AD
DF and GC
AF and AG
the porportion of interest will involve:
AC and AD, and DF and GC.
the ratio of this proportion would be:
AD / AC = DF / GC
since we know that AC = 13 and GC = 5, then we can substitute to get:
AD / 13 = DF / 5
if we multiply both sides of this equation by 13, then we get:
AD = (13 * DF) / 5
since we know that DF = DG, we can substitute to get:
AD = (13 * DG) / 5
since we know that AD + DG = 12, then we can solve for DG to get:
DG = 12 - AD which we can substitute in our equation to get:
AD = (13 * (12 - AD)) / 5
we simplify this to get:
AD = (13*12 - 13*AD)/5
we simplify further to get:
AD = (156 - 13*AD) / 5
we simplify even further to get:
AD = 31.2 - 2.6*AD
we add 2.6*AD to both sides of the equation to get:
3.6*AD = 31.2
we divide both sides of the equation by 3.6 to get:
AD = 8.66666666667 which is the same as 8 and 2/3.
since AD and GD are equal to 12, this makes GD equal to 3 and 1/3.
since DF is equal to GD, this makes DF equal to 3 and 1/3.
since DF and GD are also radii to the circle and to the sphere, this makes the radius of the sphere equal to 3 and 1/3.
the similar triangles that were formed are shown in the following diagram:
a picture of what the sphere inscribed in the cone would look like is shown below:
http://www.google.com/imgres?imgurl=http://www.math.unl.edu/~s-bkell1/103-2008f/sphere-in-cone-big.png&imgrefurl=http://www.math.unl.edu/~s-bkell1/103-2008f/challenge.html&h=772&w=522&sz=70&tbnid=pX-gNPjAroRSDM:&tbnh=90&tbnw=61&prev=/search%3Fq%3Dsphere%2Binscribed%2Bin%2Ba%2Bcone%2Bpicture%26tbm%3Disch%26tbo%3Du&zoom=1&q=sphere+inscribed+in+a+cone+picture&docid=PE4qDTHfJOECfM&hl=en&sa=X&ei=vHX4TpPsOOn20gHc4az6BQ&ved=0CEIQ9QEwCg&dur=29
|
|
|
| |