|
Question 550062: Determine the equation of the parabola with a directrix of x + y - 6 = 0 and a focus at (0, 0)
Answer by Edwin McCravy(20059)   (Show Source): (Show Source):
You can put this solution on YOUR website! Determine the equation of the parabola with a directrix of x + y - 6 = 0 and a focus at (0, 0)
We sketch the directrix line:
 The focus is the origin (0,0), so we sketch what we think the parabola might
look like. A parabola is the set of points that are the same distance
from the focus as to the directrix, so it passes so that it curvers around
the focus with the directrix outside the parabola, something like this
red curve:
The focus is the origin (0,0), so we sketch what we think the parabola might
look like. A parabola is the set of points that are the same distance
from the focus as to the directrix, so it passes so that it curvers around
the focus with the directrix outside the parabola, something like this
red curve:
 We pick an arbitrary point on our sketched parabola, and label it
P(x,y)
We pick an arbitrary point on our sketched parabola, and label it
P(x,y)
 From that arbitrary point, we draw a line from it perpendicular to the
directrix, labeling its distance d1. Then we draw another line
from that arbitrary point P to the focus (0,0), and label its distance d2:
From that arbitrary point, we draw a line from it perpendicular to the
directrix, labeling its distance d1. Then we draw another line
from that arbitrary point P to the focus (0,0), and label its distance d2:
 In order for the red curve to be a parabola, we must have
d1 = d2
To find d1, we need the formula from a point to a line,
The formula for the distance d from a point (x1, y1) to a line whose equation is
Ax + By + C = 0
is given by the formula:
d =
In order for the red curve to be a parabola, we must have
d1 = d2
To find d1, we need the formula from a point to a line,
The formula for the distance d from a point (x1, y1) to a line whose equation is
Ax + By + C = 0
is given by the formula:
d = 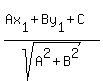 Therefore
d1 =
Therefore
d1 = 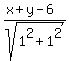 = = 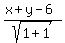 = = 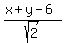 To find d2, we need the formula for the distance between two
points,
The formula for the distance d between two points (x1, y1) and (x2, y2)
is given by the formula
d =
To find d2, we need the formula for the distance between two
points,
The formula for the distance d between two points (x1, y1) and (x2, y2)
is given by the formula
d = 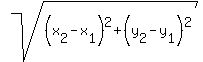 Therefore
d2 =
Therefore
d2 = 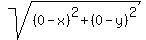 d2 =
d2 = 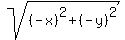 d2 =
d2 =  Now we set
d1 = d2
Now we set
d1 = d2
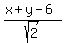 = =  We square both sides:
We square both sides:
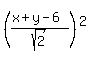 = = 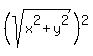
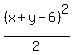 = x² + y²
Multiply both sides by 2
(x + y - 6)² = 2x² + 2y²
x² + y² + (-6)² + 2xy + 2x(-6) + 2y(-6) = 2x² + 2y²
x² + y² + 36 + 2xy - 12x - 12y = 2x² + 2y²
-x² + 2xy - y² - 12x - 12y + 36 = 0
x² - 2xy + y² + 12x + 12y - 36 = 0
Edwin = x² + y²
Multiply both sides by 2
(x + y - 6)² = 2x² + 2y²
x² + y² + (-6)² + 2xy + 2x(-6) + 2y(-6) = 2x² + 2y²
x² + y² + 36 + 2xy - 12x - 12y = 2x² + 2y²
-x² + 2xy - y² - 12x - 12y + 36 = 0
x² - 2xy + y² + 12x + 12y - 36 = 0
Edwin
|
|
|
| |