Question 549902: Working together, Pat, Lindsay, and Robin can dig a drainage ditch in 2 hours. Working alone, Robin can do it in 6 hours, while Pat can do it 2 1/4 hours faster than Lindsay. How long will it take Lindsay to dig the ditch by herself?
Answer by nerdybill(7384)   (Show Source): (Show Source):
You can put this solution on YOUR website! Working together, Pat, Lindsay, and Robin can dig a drainage ditch in 2 hours. Working alone, Robin can do it in 6 hours, while Pat can do it 2 1/4 hours faster than Lindsay. How long will it take Lindsay to dig the ditch by herself?
.
Let x = time (hours) it takes Lindsay
then
x - 2.25 = time it takes Pat
.
2(1/6 + 1/x + 1/(x-2.25)) = 1
multiplying both sides by 6x(x-2.25):
2(x(x-2.25) + 6(x-2.25) + 6x) = 6x(x-2.25)
2(x^2-2.25x + 6x-13.5 + 6x) = 6x^2-13.5
2(x^2+9.75x-13.5) = 6x^2-13.5
2x^2+19.5x-27 = 6x^2-13.5
19.5x-27 = 4x^2-13.5
-27 = 4x^2-19.5x-13.5
0 = 4x^2-19.5x+13.5
applying the quadratic formula we get:
x = {4.04, 0.84}
toss out the .84 solution (extraneous) leaving:
x = 4 hours (Lindsay's time)
.
Details of quadratic follows:
| Solved by pluggable solver: SOLVE quadratic equation with variable |
Quadratic equation  (in our case (in our case  ) has the following solutons: ) has the following solutons:

For these solutions to exist, the discriminant  should not be a negative number. should not be a negative number.
First, we need to compute the discriminant  : :  . .
Discriminant d=164.25 is greater than zero. That means that there are two solutions:  . .


Quadratic expression 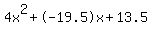 can be factored: can be factored:

Again, the answer is: 4.03950070224704, 0.835499297752963.
Here's your graph:
 |
|
|
|