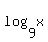 +
+ 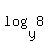 = 2
= 2
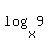 +
+ 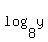 =
= 
Let u = 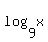 .
Then use the rule of logarithms
.
Then use the rule of logarithms  to write
to write
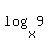 =
= 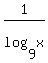 =
=  Let v =
Let v = 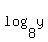 .
Then use the same rule of logarithms
.
Then use the same rule of logarithms  to write
to write
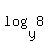 =
= 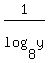 =
=  So now the system is
u +
So now the system is
u +  = 2
= 2
 + v =
+ v =  Clear each of fractions by multiplying the first thru by v and the
second one through by 3u
uv + 1 = 2v
3 + 3uv = 8u
Solve the first for uv
uv + 1 = 2v
uv = 2v - 1
Substitute for uv in the second:
3 + 3uv = 8u
3 + 3(2v-1) = 8u
3 + 6v - 3 = 8u
6v = 8u
3v = 4u
v =
Clear each of fractions by multiplying the first thru by v and the
second one through by 3u
uv + 1 = 2v
3 + 3uv = 8u
Solve the first for uv
uv + 1 = 2v
uv = 2v - 1
Substitute for uv in the second:
3 + 3uv = 8u
3 + 3(2v-1) = 8u
3 + 6v - 3 = 8u
6v = 8u
3v = 4u
v =  Substitute in
3 + 3uv = 8u
3 + 3u
Substitute in
3 + 3uv = 8u
3 + 3u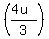 = 8u
Cancel 3's in the second term:
3 + u(4u) = 8u
3 + 4u² = 8u
4u² - 8u + 3 = 0
(2u - 3)(2u - 1) = 0
2u - 3 = 0; 2u - 1 = 0
2u = 3; 2u = 1
u =
= 8u
Cancel 3's in the second term:
3 + u(4u) = 8u
3 + 4u² = 8u
4u² - 8u + 3 = 0
(2u - 3)(2u - 1) = 0
2u - 3 = 0; 2u - 1 = 0
2u = 3; 2u = 1
u =  u =
u =  3v = 4u 3v = 4u
3v = 4
3v = 4u 3v = 4u
3v = 4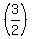 3v = 4
3v = 4 3v = 6 3v = 2
v = 2 v =
3v = 6 3v = 2
v = 2 v =  So we have (u,v) = (
So we have (u,v) = ( ,2) or (u,v) = (
,2) or (u,v) = ( ,
, )
But we want x and y, not u and v, so we substitute back in each case:
(u,v) = (
)
But we want x and y, not u and v, so we substitute back in each case:
(u,v) = ( ,2)
u =
,2)
u = 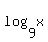 v =
v = 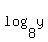
 =
= 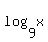 2 =
2 = 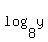 Write in exponential form using the rule:
Write in exponential form using the rule:  is equivalent to
is equivalent to  x =
x = 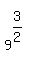 =
= 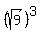 = 3³ = 27 y = 8² = 64
So one solution is (x,y) = (27,64)
For the other case:
(u,v) = (
= 3³ = 27 y = 8² = 64
So one solution is (x,y) = (27,64)
For the other case:
(u,v) = ( ,
, )
u =
)
u = 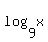 v =
v = 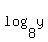
 =
= 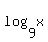
 =
= 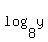 Write in exponential form using the rule:
Write in exponential form using the rule:  is equivalent to
is equivalent to  x =
x = 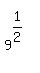 =
=  = 3 y =
= 3 y =  =
= 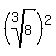 = 2² = 4
So the other solution is (x,y) = (3,4)
There are two solutions:
(x,y) = (27,64) and (x,y) = (3,4)
Edwin
= 2² = 4
So the other solution is (x,y) = (3,4)
There are two solutions:
(x,y) = (27,64) and (x,y) = (3,4)
Edwin