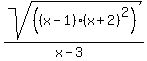
The domain is the set of all numbers that can be substituted for x
such that the result will be a defined value.
The dominator must not be 0, so we must not have x-3 = 0 or x = 3
So the domain must leave out 3
There also must be no negative numbers under the square root.
There is no concern about the (x+2)² because even if x+2 were negative,
its square would be positive. So we only have to require that x-1 be ≧ 0,
which gives x ≧ 1, so the domain on a number line is
-------------------------⚫=======⚪===========>
-5 -4 -3 -2 -1 0 1 2 3 4 5 6
and in interval notation is
 Edwin
Edwin