Question 549501: 2log(x)-log(10)-3=0
Answer by bucky(2189)   (Show Source): (Show Source):
You can put this solution on YOUR website! Given to solve: 
.
I think I'm safe in assuming that by using the term "log", you mean that the base of the logarithms you are using is 10.
.
One of the first things you can choose to do is to add +3 to both sides of this equation to get rid of the -3 on the left side and move the constant to the right side as follows:
.

.
Now you have only logarithm terms on the left side. You can apply the rules of logarithms to these terms. Begin by noting that the first logarithm term has the constant 2 multiplying it. By the rules, a multiplying constant can be taken inside the logarithm function as an exponent as shown below:
.

.
There are now two ways that you can deal with the negative logarithm. You can note that when the base of the logarithm is the same as the quantity that the logarithm is operating on, the logarithm term can be replaced by the number 1. Here are some examples:
.
 ; ;  ; ;  ; and ; and 
.
So you could immediately replace 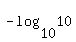 by by  and you would have: and you would have:
.

.
Then you could add 1 to both sides to get rid of the -1 on the left side. The result would be:
.

.
And you could proceed to solve for x from this point by using the conversion from logarithmic form to exponential form that I'm going to describe a little bit further on.
.
But instead of doing it that way let's do it another way that contains the lesson that the difference between two logs can be expressed as the logarithm of their division in which the denominator is the quantity that the negative logarithm term is operating on. Sounds hard, but it's pretty easy actually. Going back to the point we had arrived at, which was:
.

.
The rules of logarithms say that you can convert the two terms on the left to a single logarithm in which the quantity  from the first logarithm is divided by the quantity from the first logarithm is divided by the quantity  from the negative logarithm as follows: from the negative logarithm as follows:
.

.
Next we're going to take a look at converting logarithms to exponential form. This is an important property to learn because so many logarithm problems (like this problem) make use of it. The conversion equation says that by the definition of logarithm:
.
 is the same as saying is the same as saying 
.
This says "If you have a logarithm form, you can change it to an exponential form by taking the base of the logarithm, raising it to the exponent of the quantity on the other side of the equal sign, and setting that result equal to the quantity that the logarithm is operating on." Let's continue. We have arrived at:
.

.
Let's convert this to exponential form. Take the base (which is 10); raise it to the power of the 3 on the right side of this equation, and set that equal to 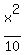 . This leads to the exponential equation: . This leads to the exponential equation:
.

.
I hope that you followed that. Now get rid of the denominator 10 by multiplying both sides of this equation by 10. On the left side multiplying
.
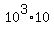
.
and by adding the exponent 3 to the exponent 1 implied for just the 10) this multiplication results in:
.
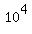
.
and on the right side, the multiplication by 10 eliminates the 10 in the denominator. So this equation has been reduced to:
.

.
Now you can solve for x simply by taking the square root of both sides. When you do that the exponent on the left side is just divided by 2 to give you the square root (think  . And on the right side the x-squared becomes just x. So we have the solution: . And on the right side the x-squared becomes just x. So we have the solution:
.

.
And the 10 squared is just 10 times 10 which is 100.
.
So the answer to this problem is x = 100.
.
Hope that this long explanation helps you to understand logarithms a little better. It's just a matter of practice and thinking about all this. It'll become easier with working on these types of problems until you get familiar with all the rules of logarithms. Keep working at it.
.
|
|
|