SOLUTION: 2. Given 20 different types of inputs to a program, in how many ways can 8 of them be selected if a) Order does not matter b) Order matters

Let's do the b) part first, where order matters:

b)
1. There are 20 ways to select the 1st input. 

2. For each of those 20 ways to select the 1st input, there are 19 ways
left to select the 2nd input.  That's 20×19 ways to select the first 2 inputs.

3. For each of those 20×19 ways to select the 1st 2 inputs,
there are 18 ways to select the 3rd input.  That's 20×19×18 ways to select the
first 3 inputs.

4. For each of those 20×19×18 ways to select the 1st 3 inputs, 
there are 17 ways left to select the 4th input.  That's 20×19×18×17 ways to
select the first 4 inputs.

5. For each of those 20×19×18×17 ways to select the 1st 4 inputs, 
there are 16 ways left to select the 5th input.  That's 20×19×18×17×16 ways to
select the first 5 inputs.

6. For each of those 20×19×18×17×16 ways to select the 1st 5 inputs, 
there are 15 ways left to select the 6th input.  That's 20×19×18×17×16×15 ways
to select the first 6 inputs.

7. For each of those 20×19×18×17×16×15 ways to select the 1st 6 inputs,
there are 14 ways left to select the 7th input.  That's 20×19×18×17×16×15×14
ways to select the first 7 inputs.

8. For each of those 20×19×18×17×16×15×14 ways to select the 1st 7 inputs, 
there are 13 ways left to select the 8th input.  That's 20×19×18×17×16×15×14×13
ways to select the first 8 inputs.  That's all of them!  So the answer is

20×19×18×17×16×15×14×13 = 5079110400

-----------------

Now let's do the a) part, where order does not matter.

Each group of 8 in which the order does not matter was ordered in
8×7×6×5×4×3×2×1 ways above among the 20×19×18×17×16×15×14×13 in which
order mattered.  Therefore the answer to b) counts each group of 8
in the a) part 8×7×6×5×4×3×2×1 times too many. So we just
need to divide the answer to part b) by 8×7×6×5×4×3×2×1 to get the 
answer for part a), and when we do we get:

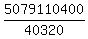 =  = 125970

The short way is, of course.

(a) 20C8 = 125970
(b) 20P8 = 5079110400

The first way is the reason WHY you do what you do.  It may not seem so, but
mathematics is easier in the long run when you understand WHY you do what you
do, not just HOW to do it.

Edwin