Question 54932: Please help me wit this problem:
Find the exact solution to the equation 3^x+5=9^x
Found 3 solutions by rapaljer, stanbon, josmiceli:
Answer by rapaljer(4671)   (Show Source): (Show Source):
Answer by stanbon(75887)   (Show Source): (Show Source):
You can put this solution on YOUR website! 3^x+5=9^x
Rewrite as:
3^(2x)-3^x-5=0
Let 3^x be "w"
Rewrite the equation in "w", as follows:
w^2-w-5=0
Use the quadratic formula to solve for "w", as follows:
w=[1+-sqrt(1+20)]/2
w=[1+-sqrt(21)]/2
Convert back to "x" notation.
3^x=[1+-sqrt(21)]/2
Take the log of both sides to get:
x(log 3)=[1+-sqrt(21)]/2
x=[1+-sqrt(21)/[2log(3)]
Cheers,
Stan H.
Answer by josmiceli(19441)   (Show Source): (Show Source):
You can put this solution on YOUR website! This might not be the shortest solution, but it seems to check OK

note that  , so , so

also,  because, if x were 5, let's say, then because, if x were 5, let's say, then


subtract 3^x from both sides

note that 

now factor out 3^x

make a substitution, let  , so , so


solve completing the square


take the square root of both sides




since 

take the log of both sides. I chose log to the base e.



 answer answer
I'll sub this back into the original equation




This is true up to the 5th decimal place, so I believe the error is due
to my rounding off on calculator
Note also that I could have used the negative square root of 21
in the calculation for z, but this would have made 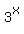 negative, negative,
and that's impossible, no matter what x is.
|
|
|