Question 549172: what is a good definition of irrational and rational numbers
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! DISCLAIMER - PERSONAL BELIEF, not official definition:
To me, a rational number is one that is equivalent to the ratio of two integers.
An irrational number is a number that is not rational, but we need to say it's real because it is a needed boundary between sets, or sequences of rational numbers. For example, we can calculate infinity of rational numbers, x, such that 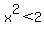 , and infinity or rational numbers, y such that , and infinity or rational numbers, y such that 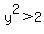 . We can find pairs (x,y) as close together as we want. There has to be a number at the boundary between the x's and the y's, but we cannot find a rational number that fits the bill. So we say that the number exists, it's real, but it is not rational. We call it irrational, and we represent it as . We can find pairs (x,y) as close together as we want. There has to be a number at the boundary between the x's and the y's, but we cannot find a rational number that fits the bill. So we say that the number exists, it's real, but it is not rational. We call it irrational, and we represent it as  . For other irrational numbers, we cannot even find an analogy so that we can write them as an operation, like square root, on a rational number, and we have to invent a name like . For other irrational numbers, we cannot even find an analogy so that we can write them as an operation, like square root, on a rational number, and we have to invent a name like  or or  . .
|
|
|