SOLUTION: Solve X^2 + 11 = 6x

Algebra ->  Quadratic Equations and Parabolas -> SOLUTION: Solve X^2 + 11 = 6x      Log On


   

Question 549064: Solve X^2 + 11 = 6x
Found 2 solutions by jim_thompson5910, KMST:
Answer by jim_thompson5910(35256) About Me  (Show Source):
You can put this solution on YOUR website!
x%5E2%2B11=6x Start with the given equation.


x%5E2%2B11-6x=0 Get every term to the left side.


x%5E2-6x%2B11=0 Rearrange the terms.


Notice that the quadratic x%5E2-6x%2B11 is in the form of Ax%5E2%2BBx%2BC where A=1, B=-6, and C=11


Let's use the quadratic formula to solve for "x":


x+=+%28-B+%2B-+sqrt%28+B%5E2-4AC+%29%29%2F%282A%29 Start with the quadratic formula


x+=+%28-%28-6%29+%2B-+sqrt%28+%28-6%29%5E2-4%281%29%2811%29+%29%29%2F%282%281%29%29 Plug in A=1, B=-6, and C=11


x+=+%286+%2B-+sqrt%28+%28-6%29%5E2-4%281%29%2811%29+%29%29%2F%282%281%29%29 Negate -6 to get 6.


x+=+%286+%2B-+sqrt%28+36-4%281%29%2811%29+%29%29%2F%282%281%29%29 Square -6 to get 36.


x+=+%286+%2B-+sqrt%28+36-44+%29%29%2F%282%281%29%29 Multiply 4%281%29%2811%29 to get 44


x+=+%286+%2B-+sqrt%28+-8+%29%29%2F%282%281%29%29 Subtract 44 from 36 to get -8


x+=+%286+%2B-+sqrt%28+-8+%29%29%2F%282%29 Multiply 2 and 1 to get 2.


x+=+%286+%2B-+2i%2Asqrt%282%29%29%2F%282%29 Simplify the square root (note: If you need help with simplifying square roots, check out this solver)


x+=+%286%29%2F%282%29+%2B-+%282i%2Asqrt%282%29%29%2F%282%29 Break up the fraction.


x+=+3+%2B-+i%2Asqrt%282%29 Reduce.


x+=+3%2Bi%2Asqrt%282%29 or x+=+3-i%2Asqrt%282%29 Break up the expression.


So the solutions are x+=+3%2Bi%2Asqrt%282%29 or x+=+3-i%2Asqrt%282%29


If you need more help, email me at jim_thompson5910@hotmail.com

Also, please consider visiting my website: http://www.freewebs.com/jimthompson5910/home.html and making a donation. Thank you

Jim

Answer by KMST(5328) About Me  (Show Source):
You can put this solution on YOUR website!
x%5E2%2B11=6x is a quadratic equation.
In the (equivalent) traditional form to present a quadratic equation, it would be
x%5E2-6x%2B11=0
SHORT ANSWER:
The discriminant b%5E2-4ac=%28-6%29%5E2-4%2A1%2A11=36-44=-4 is negative, so there are no real solutions.
LONG GENERAL EXPLANATION ON QUADRATIC EQUATIONS:
There are many approaches to solve quadratic equations:
You could factor, graph, apply the quadratic formula, or "complete the square,"
Factoring does not work all the time. It only works when the solutions are rational numbers (not the case for this equation) and, even in cases where it would work, it is an approach that takes some practice.
Graphing adds to your understanding, and it will work sometimes, but it is useful mainly if you have a graphing calculator or other graphing software, and the exact answer is not required.
QUADRATIC FORMULA:
Using the quadratic formula works every time, without needing to think much, but requires using the complicated looking quadratic formula:
x+=+%28-b+%2B-+sqrt%28+b%5E2-4%2Aa%2Ac+%29%29%2F%282%2Aa%29+
The expression under the square root is called the discriminant, and it is good to calculate that part first.
discriminant=b%5E2-4%2Aa%2Ac
After that, the quadratic formula simplifies into
x=%28-b+%2B-+sqrt%28discriminant%29%29%2F%282%2Aa%29
You can see that the quadratic formula will not give you a real solution if the discriminant is negative. You would answer that there are no real solutions.
You can see that the quadratic formula simplifies into x+=-b+%2F%282%2Aa%29 when the discriminant is zero.
If the discriminant is positive, you will get two real solutions.
You can identify the values for a, b, and c, by comparing the coefficients in your equation to those in the generic quadratic equation
ax%5E2%2Bbx%2Bc=0
The coefficient of the term in x%5E2 is a. If it's just x%5E2 with no visible coefficient, a=1. If it's just -x%5E2, then a=-1.
The coefficient of x is b. If nothing is visible in front of an x, b could be 1, or -1, as with a. If you don't even see a term in x, b=0.
The independent term (the term without x) is c. If you don't see an independent term, then c=0.
For x%5E2-6x%2B11=0, a=1, b=-6, and c=11
The discriminant, b%5E2-4ac=%28-6%29%5E2-4%2A1%2A11=36-44=-4, is negative, so there are no real solutions. (If you are allowed to work with imaginary numbers, you could calculate two complex solutions using the quadratic formula).
COMPLETING THE SQUARE
"Completing the square" takes some practice, and could be difficult at times, but it does not require memorizing formulas, and would work easily in this case. I'll demonstrate.
We can write the equation with the terms containing x on one side of the equal sign, and the term without x on the other side:
x%5E2-6x%2B11=0 ---> x%5E2-6x=-11
At this point, we try to imagine 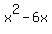x%5E2-6x as part of the square of a binomial and see that
x%5E2-6x%2B9=%28x-3%29%5E2
We add 9 to both sides of the equation x%5E2-6x=-11 to get
x%5E2-6x%2B9=-11%2B9 <---> %28x-3%29%5E2=-2
There is no happy ending here, because at this point we realize that there are no real solutions, because the square of a real number is never negative.
If we are allowed to work with imaginary numbers, we can continue on to x=3+%2B-+isqrt%282%29. Otherwise, we just say that there are no real solutions.