SOLUTION: sketch a graph at 4x^2-3xy=18 and identify the angle of rotation

Algebra ->  Graphs -> SOLUTION: sketch a graph at 4x^2-3xy=18 and identify the angle of rotation       Log On


   

Question 549004: sketch a graph at 4x^2-3xy=18 and identify the angle of rotation
Answer by Edwin McCravy(20066) About Me  (Show Source):
You can put this solution on YOUR website!
4x² - 3xy = 18
 
We write it in the form of the general conic:
 
Ax² + Bxy + Cy² + Dx + Ey + F = 0
 
4x² - 3xy + 0y² + 0x + 0y - 18 = 0
 
So A=4, B=-3, C=0, D=0, E=0, F=-18
 
To find the angle to rotate the graph, we use:
 
tan(2Ɵ) = 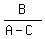B%2F%28A-C%29 
 
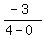tan(2Ɵ) = %28-3%29%2F%284-0%29
 
tan(2Ɵ) = -3%2F4
 
Use the identity for tan(2Ɵ)
 
tan(2Ɵ) = 2tan%28theta%29%2F%281-%22tan%22%5E2%28theta%29%29
 
2tan%28theta%29%2F%281-%22tan%22%5E2%28theta%29%29 = -3%2F4
 
8tanƟ = -3(1 - tan²Ɵ)
 
8tanƟ = -3 + 3tan²Ɵ
 
-3tan²Ɵ + 8tanƟ + 3 = 0
 
3tan²Ɵ - 8tanƟ - 3 = 0
 
That factors:
 
(tanƟ - 3)(3tanƟ + 1) = 0
 
tanƟ - 3 = 0          3tanƟ + 1 = 0  
                         
    tanƟ = 3               tanƟ = -1%2F3
 
       Ɵ = arctan(3)          Ɵ = arctan(-1%2F3)
                    
   Ɵ = 71.56505118°           Ɵ = 161.5650512° or 341.5650512° 
       or 251.5650512°
 
Either of those angles will eliminate the xy term when rotated through
them.  We choose Ɵ = arctan(3) = 71.56505118°.
 
We draw the triangle:   and use the Pythagorean theorem to find the hypotenuse:  
 
 Next we substitute 

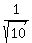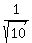x = x'cosƟ-y'sinƟ = x'1%2Fsqrt%2810%29-y'3%2Fsqrt%2810%29 = 1%2Fsqrt%2810%29(x' - 3y') 
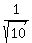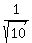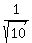y = x'sinƟ+y'cosƟ = x'3%2Fsqrt%2810%29+y'1%2Fsqrt%2810%29 = 1%2Fsqrt%2810%29(3x' + y') 


in

4x² - 3xy = 18
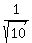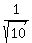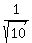4(1%2Fsqrt%2810%29(x' - 3y'))² - 3(1%2Fsqrt%2810%29(x' - 3y'))(1%2Fsqrt%2810%29(3x' + y')) = 18

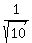4(1%2Fsqrt%2810%29)²(x' - 3y')² - 3(1%2Fsqrt%2810%29)²(x' - 3y')(3x' + y') = 18

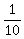4(1%2F10)(x' - 3y')² - 3(1%2F10%29)(x' - 3y')(3x' + y') = 18

Multiply through by 10

4(x' - 3y')² - 3(x' - 3y')(3x' + y') = 180

4(x'² - 6x'y' + 9y'²) - 3(3x'² - 8x'y' - 3y'²) = 180

4x'² - 24x'y' + 36y'² - 9x'² + 24x'y' + 9y'² = 180
 
-5x'² + 45y'² = 180

Divide through by 180 to get 1 on the right side

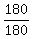
%28-5%29%2F180x'² + 45%2F180y'² = 180%2F180

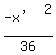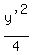%22-x%27%22%5E2%2F36 + %22y%27%22%5E2%2F4 = 1

Write the positive term first:

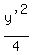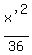%22y%27%22%5E2%2F4 - %22x%27%22%5E2%2F36 = 1

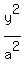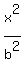This is a hyperbola of the form y%5E2%2Fa%5E2 - x%5E2%2Fb%5E2 = 1
rotated through an angle of Ɵ = arctan(3) = 71.56505118°.
a = 2 and b = 6

We will draw the x' and y' axes in green:

 

We draw in the defining rectangle, 6 units out the x' axis in
both directions, and 2 units out the y' axis in both directions. 


 

We draw in the asymptotes as the extended diagonals of the
defining rectangle, one of which turns out to be the y-axis:



And we sketch in the hyperbola:






 
 Edwin