Question 548928: Determine all positive integers n for which 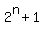 is divisible by 3. is divisible by 3.
Answer by mathie123(224)   (Show Source): (Show Source):
You can put this solution on YOUR website! We can test for the first few values of n (n=0, n=1, n=2, n=3, n=4...) and see a pattern emerging. It seems that when n is odd, 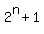 is divisible by 3. is divisible by 3.
We can use induction to prove that this is true for all even values of n.
We have tried base cases, so it holds for the base cases.
Since any even number can be written as 2k where k is an integer, we will assume that for all values up to k, 2^{2*k}+1=3*m (m is an integer, meaning it is divisble by 3.
This can be rewritten as:
2^{2(k)}=3m-1
We must now prove that 2^{2(k+1)}+1 is divisible by 3.
2^{2(k+1)}+1
=2^(2k)*2^2+1
=4*(3m-1)+1
=12m-4+1
=12m-3
Now since both 12 and -3 are divisible by 3, then this whole value is divisible by three.. so our proof is done
Hopefully this helps, let me know if you are still unsure :)
|
|
|