SOLUTION: Maximization Maximize p = 7x - 4y subject to y >= 2x - 8 y <= 10 - x y <= (x + 8) / 2 x >= 1 y >= 2 Thank you

Algebra ->  Graphs -> SOLUTION: Maximization Maximize p = 7x - 4y subject to y >= 2x - 8 y <= 10 - x y <= (x + 8) / 2 x >= 1 y >= 2 Thank you      Log On


   

Question 548268: Maximization
Maximize p = 7x - 4y subject to
y >= 2x - 8
y <= 10 - x
y <= (x + 8) / 2
x >= 1
y >= 2
Thank you
Found 2 solutions by mathie123, Edwin McCravy:
Answer by mathie123(224) About Me  (Show Source):
You can put this solution on YOUR website!
I will first look at the equations (I rewrote (3) a bit... if you don't see what I did let me know):
y+%3E=+2x+-+8 (1)
y+%3C=+10+-+x (2)
y+%3C=+%281%2F2%29%2Ax+%2B+4 (3)
(2)-(3) leaves:
0%3C=6-%283%2F2%29%2Ax
%283%2F2%29%2Ax%3C=6
3x%3C=12
x%3C=4

Equation (1) can be rewritten as
-y%3C=-2x%2B8 (4)
Equation (4) +equation (2) gives
0%3C=18-3x
3x%3C=18
x%3C=6 (Note: we already know x<=4... so this is no surprise...)
Equation (4)+ Equation(3) gives
0%3C=%28-3%2F2%29%2Ax%2B12
%283%2F2%29%2Ax%3C=12
3x%3C=24
x%3C=8 (Again... no surprise... but it's good to check as we could have gotten a different value)
So we know now that 1%3C=x%3C=4.(So the maximum value of x is 4)

We have to do the same thing for y by eliminating x
Just a reminder:
y+%3E=+2x+-+8 (1) which is really just -y%3C=-2x%2B8 (4)
y+%3C=+-x%2B10 (2)
y+%3C=+%281%2F2%29%2Ax+%2B+4 (3)
Let's first compare (4) and (2)
We need to eliminate x so I will multiply equation (2) by 2 to get:
2y%3C=-2x%2B20 (5)
So adding (4) and (5) we get
y%3C=+28
Now let's compare (1) and (3)
We will first multiply equation (3) by -4 to get ((WHEN MULTIPLYING OR DIVIDING BY A NEGATIVE NUMBER, YOU MUST CHANGE INEQUALITY SIGN))
-4y%3E=-2x-16 (6)
Now adding (6) to (1) we get
-3y%3E=-24
y%3C=8
One more comparison... (2) and (3)
We will multiply (3) by -2 (and switch the sign) to get:
-2y%3E=-x-8 (7)
Now we want to compare (7) with (2) but first we must rearrange (2) so the inequality signs match
y+%3C=+-x%2B10 (2)
-y%3E=x-10 (8)
And finally adding (7) and (8) we get
-3y%3E=-18
y%3C=6 (This is a surprise!)
So if all these must be true we have 2%3C=y%3C=6 and the maximum bound on y is 6.

To maximize p we must sub in both our maximum x and maximum y into the formula p=7x-4y... I will let you do this part:)

Phew! Hopefully this helps!




Answer by Edwin McCravy(20056) About Me  (Show Source):
You can put this solution on YOUR website!
The other tutor apparently didn't understand what you want.
We draw the lines

y=2x-8, y=10-x, y=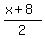%28x%2B8%29%2F2, x=1, and y=2 

 

Maximization 
Maximize p = 7x - 4y subject to
y ≧ 2x - 8,  the red line y=2x-8 and the region above it, since it's y≧
y ≦ 10 - x, the green line y=10-x and the region below it, since it's y≦
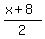y ≦ %28x+%2B+8%29%2F2, the blue line y=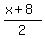%28x%2B8%29%2F2 and the region below it, since it's y≦
x ≧ 1, the black line x=1 and the region to the right of it, since it's x≧
y ≧ 2, the purple line y=2 and the region above it, since it's y≧


We will chop off the unnecessary parts of the lines, leaving 
only the region bounded by them, which is this pentagon:

 

Now we must find all the corner points of this pentagon, by solving these
five systems:

system%28y=2x-8%2C10-x%29 the red and green lines, which gives (6,4)
system%28y=2x-8%2Cy=2%29 the red and purple lines, which gives (5,2)
system%28x=1%2Cy=2%29 the black and purple lines, which gives (1,2)
system%28y=%28x%2B8%29%2F2%2Cx=1%29 the blue and black lines, which gives (1,4.5).
system%28y=10-x%2Cy=%28x%2B8%29%2F2%29 the blue and green lines, which gives (4,6)


 
We evaluate p = 7x - 4y at each of those corner points:

Corner point | p = 7x - 4y
    (1,2)    |     -1
    (5,2)    |     27
    (6,4)    |     26
    (4,6)    |      4
  (1,4.5)    |    -11

So the maximum value of p=27 occurs when x=5 and y=2

Edwin