Question 548265: Maximization
Maximize p = 2x + 4y subject to
x >= 0, y >= 0, 2x - y >= 2 and x + 2y <= 8
Help me. I don't know how to do it.
The answer is: The function is maximum at (8,0) et (12/5, 14/5) and is worth 16.
Thank you
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! This type of problem requires knowing about linear functions, linear equations, inequalities, and graphing. I'll give you some tips and tricks at the end.
Normally, a linear optimization problem like this one includes a lot of calculations and graphing, and you end up finding the maximum at a corner. In this case the maximum is all along the side of a triangle, but the problem is easy if you do not have to show your work. As a consequence, I can skip a few calculations. But I'll show you (at the end) how to work through any optimization problem, even when you have to show your work, including the calculations and graphing that I could avoid in this problem when no one was making me do them. (Feel free to skip that part if you already know all that, and were only puzzled by the maximum not being just at one point, or by the way the solution is expressed).
You are supposed to work within the boundaries
 , ,  , ,  , and , and  , the axes and two slanted lines. , the axes and two slanted lines.
The function of x and y to be maximized  will take a given value, such as will take a given value, such as  along a straight line. In the case of along a straight line. In the case of  , it would be the line , it would be the line  . It's obvious that if you increase both x and y, you will increase p. So, as we get away from the origin we increase p, and to maximize p, we we have to get as far away from the origin as we can (within the boundaries set). . It's obvious that if you increase both x and y, you will increase p. So, as we get away from the origin we increase p, and to maximize p, we we have to get as far away from the origin as we can (within the boundaries set).
If we graphed the lines  for various p values, they would be all parallel. In fact, one of those lines for various p values, they would be all parallel. In fact, one of those lines  is the boundary line is the boundary line  . .
They are equivalent equations. If you multiply both sides of  by 2, you get by 2, you get  . .
The maximum p will be 16 and will happen all along a portion of the boundary line  , a segment of that line. , a segment of that line.
We just need to find the ends of that segment, which will happen when the line  intersects the x-axis, and when the line intersects the x-axis, and when the line  intersects the line intersects the line  . .
The line  (the x-axis), and the line (the x-axis), and the line  intersect at intersect at  , of course, which we find by substituting , of course, which we find by substituting  into into  . That gives us the point (8,0). . That gives us the point (8,0).
The intersection of lines  and and  requires solving the system of equations formed by those 2 equations. requires solving the system of equations formed by those 2 equations.
Solving for y in  --> --> 
and substituting in  would work. would work.
We get  --> -->  and and  , ,
which we substitute into  to get to get
 . .
That gives us the point (12/5,14/5) where the slanted lines intersect.
SOLUTION: The function is maximum at the segment between points (8,0) and (12/5, 14/5) and is worth 16.
THE GRAPH that I only needed to draw in my mind
Our boundaries include the x- and y-axis, and the inequalities
 and and  tell you that you are working in the first quadrant. tell you that you are working in the first quadrant.
The other two boundaries are linear equations, and I can tell (without calculating anything) that the x- and y-intercepts for those lines will be positive except for (0,-2), the y-intercept for  . .
The origin, point (0,0), satisfies  , but not , but not  , so I know we are working on the side of , so I know we are working on the side of  that contains the origin, and at the same time, on the side of that contains the origin, and at the same time, on the side of  that does not contain the origin. that does not contain the origin.
It looks like this:
 and we are working in the triangle between the x-axis and the slanted lines. and we are working in the triangle between the x-axis and the slanted lines.
TIPS AND TRICKS
Graphing is easier when done on graph paper.
Expect your first attempt at doing a graph to be a rough draft that will need to be improved upon (change of scale, better choice of points to plot, calculation errors, etc).
To graph a line you only need to points. You want them to be easy to calculate, and easy to plot, spaced far enough to draw the line accurately, and located within your graph.
Often you can get one or two good line points to plot by substituting  and and  in the equation of a line. For in the equation of a line. For  , you get (0,4) and (8,0) that way, and those are excellent points to graph that line. For , you get (0,4) and (8,0) that way, and those are excellent points to graph that line. For  you get (0,-2) and (2,0), which are also pretty good. you get (0,-2) and (2,0), which are also pretty good.
To graph inequalities like 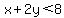 or or  , after graphing the line for , after graphing the line for  , you need to decide which side of the line is the answer. Choosing an easy test point usually works well. You want a test point that is not on the boundary line, and makes calculations easy. If possible, use (0,0), the origin. Substitute its coordinates, and see if the point is a solution. Since , you need to decide which side of the line is the answer. Choosing an easy test point usually works well. You want a test point that is not on the boundary line, and makes calculations easy. If possible, use (0,0), the origin. Substitute its coordinates, and see if the point is a solution. Since  , I know that the solution to , I know that the solution to 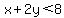 is the portion of the graph on the side of is the portion of the graph on the side of 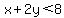 that contains the origin. For that contains the origin. For  or or 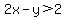 , test point (0,0) tells me that the solution is the side that does not contain the origin, because , test point (0,0) tells me that the solution is the side that does not contain the origin, because  does not satisfy those inequalities. In the case of does not satisfy those inequalities. In the case of  or or  , test point (1,1) would work well for both. Want to verify that the triangle be tween the two slanted lines and the x-axis is the feasibility region we must work in? Just check using test point (3,1). You'll see that it satisfies all the inequalities given as constraints. , test point (1,1) would work well for both. Want to verify that the triangle be tween the two slanted lines and the x-axis is the feasibility region we must work in? Just check using test point (3,1). You'll see that it satisfies all the inequalities given as constraints.
If you have to show your work in a linear optimization problem, you'll need to graph your boundary lines, and calculate their intersection points. Then you'll have to calculate the value of the function at all the intersection points and figure out a winner. If two points are tied for optimum value, they should be points that are connected by a segment of boundary line, and the maximum happens for all the points in that whole segment. In the case of this problem, you would calculate the value of p at (2,0) as  , the value at (8,0) as , the value at (8,0) as  , and the value at (12/5,14/5) as , and the value at (12/5,14/5) as  to find your solution. to find your solution.
You may be able to find the intersection points from the graph, without having to solve a system of equations. It works well when the coordinates of the intersection point seem to be integers. Make sure that the point the graph suggests as the intersection is really part of the two lines by substituting the coordinates in the equations for both lines. It would not have worked for this problem, because we could never have guessed from the graph that the intersection point was (12/5,14/5).
|
|
|