Question 548184: A freely falling body travels a distance 'x' in nth second.In the next second if it travels a distance 'y'.Which of the following is correct and why?
a) x+y=g
b) x-y=g
c) y-x=g
d) x=y
Answer by bucky(2189)   (Show Source):
You can put this solution on YOUR website! The equation for the distance a body has fallen in time t is:
.
.
In which t is the total time in seconds that has elapsed since the body started to fall, g represents the acceleration due to gravity (usually in meters per second or feet per second), and D is the total distance that the body has fallen at time t (in meters or in feet, depending on the units used for g).
.
Here's a little test-taking strategy. This problem can be solved by using actual time intervals, and this way of solving it is likely to be faster and easier than solving the problem by involving the nth time interval. The possible answers that are given tell you that you can select any two consecutive intervals and the results will be the same.
.
The problem tells you to use x for the first interval of 1 second and y for the next interval of 1 second.
.
So let's just use the first second as the time interval from t = 0 to t = 1 second. At t = 0 the body has not begun to fall, so the distance it has fallen is zero. By t = 1 second the body has fallen a distance of:
.
.
Notice that the time that the distance the body is down at one second is found by substituting 1 for t in the equation. Multiplying everything out on the right side of this equation results in:
.
.
And the distance the body has fallen during this first second if found by subtracting its distance at one second from its distance at zero seconds (which we know is zero) and we get for x (the distance fallen in the first second) is
.
.
This simplifies to just:
.
.
Next we solve for y (the distance that the body falls during the interval from 1 second to 2 seconds). We already know that at the start of this interval (that is at time t = 1 second) the position of the body is:
.
.
At the time t = 2 seconds the position of the body can be found by substituting 2 for t in the distance equation to get:
.
.
We square the time in the numerator (to get 4) and divide it by the 2 in the denominator the result is that at 2 seconds the body has fallen a total distance of:
.
.
Now all we have to do to solve for y (the distance fallen in the second time interval) is to take this distance at time equals 2 and subtract from it the distance at time equals 1 (which we already found was g/2) and we have:
.
.
and this simplifies by subtracting these two terms to give:
.
.
So at this point we have and
.
Next all we have to do is substitute these two values into the possible answers and find out which answer is correct.
.
Obviously x does not equal y, so the last answer in the list (x = y) can be eliminated easily.
.
How about the first answer on the list, 
.
Substituting for x and y that would give 
.
The answer is on the right side of this equation. Dividing the denominator (2) into the numerator (4g) is 2g not g, so that doesn't work and cannot be correct.
.
The next answer is 
.
This time, substituting for x and y would give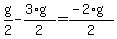 
.
The answer that results from dividing the denominator (2) into the numerator (-2g) is -g not +g, so that doesn't work and cannot be correct.
.
Finally, let's try the next answer 
.
And substituting  for y and  for x results in:
.
.
The answer that results from dividing the denominator (2) into the numerator (2g) is +g, so this answer does work and, therefore, is the correct answer.
.
Hope this helps you see a way how this problem can be done. If you feel that your teacher wants to see it done for any two consecutive time intervals in general, here is what you need to do:
.
Use t = n for the start of the first interval. This will give you  at the start of this interval.
.
Next use t = n + 1 for the end of the first interval (as well as for the start of the second interval). The result will be that the distance at the end of the first interval is given by:
.
 and this equals  . This becomes:
.
.
So the distance X that is traveled between t = n and t = n + 1 is the difference between the distances at these two times as follows:
.
 and this becomes 
.
Then use t = n + 2 for the end of the next interval. Substitute n + 2 into the distance equation to find that at time n + 2 seconds the total distance traveled at n + 2 seconds is:
.
 and that expands to  which becomes:
.
.
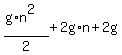
Then subtract from that answer the answer you got for the distance at the end of the first interval, namely the answer for the equation:
.
.
The result of this subtraction will be y as follows:
.
.
And this simplifies to:
.
.
Recall that the answer we found to be correct by doing it the first way was y – x = g
.
Let’s try that answer again using these new results  and 
.
Substituting for y and x results in:
.
.
And this simplifies to:
.
 which becomes
.
This is the more general way of showing that the correct answer is y – x = g
.
Check my math in all of this just to ensure that I didn't make some mistakes in signs or something else equally as careless.
|
|
|
