Question 547248: Trains A and B are traveling in the same direction on parallel tracks. Train A is traveling at 80 miles per hour and train B is traveling at 90 miles per hour. Train A passes a station at 10:10 P.M. If train B passes the same station at 10:40 P.M. at what time will train B catch up to train A?
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! At 10:40 PM, train B will be 0 miles past the station.  hours after that, it will be hours after that, it will be  miles past the station. miles past the station.
At 10:40 PM, train A will be 40 miles past the station, after traveling away from that station for 30 minutes (0.5 hours), covering 40 miles since 10:10 PM.  hours after 10:40 PM, train A will be hours after 10:40 PM, train A will be 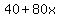 miles away from that station. miles away from that station.
At some point they will be the same distance from that station, and train B will be overtaking train A. At that point, we will have:
 --> -->  --> --> 
So, 4 hours after 10:40 PM, both trains will be at the same distance from the station and a few passengers in train B will be waving at a few passengers in train A, as B passes A. The rest of the passengers will probably be asleep, because it will be 2:40 AM.
|
|
|