SOLUTION: "A HOSE can fill a swimming pool in 6 hours. Another HOSE needs three more hours than the two HOSES combined. How long would it take for the second PIPE to fill the tank?

Algebra ->  Rate-of-work-word-problems -> SOLUTION: "A HOSE can fill a swimming pool in 6 hours. Another HOSE needs three more hours than the two HOSES combined. How long would it take for the second PIPE to fill the tank?      Log On


   

Question 547151: "A HOSE can fill a swimming pool in 6 hours. Another HOSE needs three more hours than the two HOSES combined. How long would it take for the second PIPE to fill the tank?
Found 2 solutions by Edwin McCravy, richwmiller:
Answer by Edwin McCravy(20055) About Me  (Show Source):
You can put this solution on YOUR website!
A hose can fill a swimming pool in 6 hours. Another hose needs three more hours than the two hoses combined. How long would it take for the second pipe to fill the tank?
Make this chart:
                   Number of        Hours          Rate 
                   swimming       Required          in
                 pools filled      to fill      pools/hr
1st hose                             
2nd hose                             
both combined

Let x be the number of hours required for the 2nd hose.
Fill that in for the time for the second hose, and fill in
the given 6 hours for the 1st hose.


                   Number of        Hours          Rate 
                   swimming       Required          in
                 pools filled      to fill      pools/hr
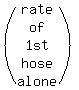
1st hose alone                        6

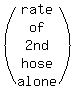
2nd hose alone                        x

both combined

>>...Another hose needs three more hours than the two hoses combined...<<
Let's re-interpret that as:

>>...The two hoses combined takes three hours less than the 2nd hose alone...<<
So we fill in x-3 for the hours for them combined:

                   Number of        Hours          Rate 
                   swimming       Required          in
                 pools filled      to fill      pools/hr
1st hose alone                        6

2nd hose alone                        x

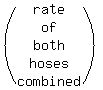
both combined                        x-3

In each case exactly 1 pool was filled, so put 1 for the
number of swimming pools filled in each case:

                   Number of        Hours          Rate 
                   swimming       Required          in
                 pools filled      to fill      pools/hr
1st hose alone        1               6

2nd hose alone        1               x

both combined         1              x-3

Fill in the rates in pools/hr by dividing pools filled by hours:

                   Number of        Hours          Rate 
                   swimming       Required          in
                 pools filled      to fill      pools/hr
1st hose alone        1               6            1%2F6
2nd hose alone        1               x            1%2Fx
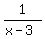both combined         1              x-3          1%2F%28x-3%29 

            The equation comes from:

              %28matrix%285%2C1%2Crate%2Cof%2C1st%2Chose%2Calone%29%29 + %28matrix%285%2C1%2Crate%2Cof%2C2nd%2Chose%2Calone%29%29 = %28matrix%285%2C1%2Crate%2Cof%2Cboth%2Choses%2Ccombined%29%29    

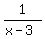              1%2F6 + 1%2Fx = 1%2F%28x-3%29

Solve that and get 6 hours

Edwin

Answer by richwmiller(17219) About Me  (Show Source):
You can put this solution on YOUR website!
It is a hose or pipe? Make up your mind!
x/6+x/y=1
y=3+x
x=3
y=6
three hours together and each of them take 6 hours alone