Question 546890: 1. In this problem, we analyze the profit found for sales of decorative tiles. A demand equation (sometimes called a demand curve) shows how much money people would pay for a product depending on how much of that product is available on the open market. Often, the demand equation is found empirically (through experiment, or market research).
a. Suppose a market research company finds that at a price of p = $31, they would sell x = 25 tile sets each month. If they lower the price to p = $6, then more people would purchase the tiles, and they can expect to sell x = 150 tile sets in a month’s time. Find the equation of the line for the demand equation. Write your answer in the form p = mx + b. Hint: Write an equation using two points in the form (x,p).
A company’s revenue is the amount of money that comes in from sales, before business costs are subtracted. For a single product, you can find the revenue by multiplying the quantity of the product sold, x, by the demand equation, p.
b. Substitute the result you found from part a. into the equation R = xp to find the revenue equation. Provide your answer in simplified form.
The costs of doing business for a company can be found by adding fixed costs, such as rent, insurance, and wages, and variable costs, which are the costs to purchase the product you are selling. The portion of the company’s fixed costs allotted to this product is $600, and the supplier’s cost for a set of tile is $2 each. Let x represent the number of tile sets.
c. If b represents a fixed cost, what value would represent b?
d. Find the cost equation for the tile sets. Write your answer in the form C = mx + b.
Answer by KMST(5328)   (Show Source):
You can put this solution on YOUR website! a. A market research company finds that at a price of p = $31, they would sell x = 25 tile sets each month. If they lower the price to p = $6, then more people would purchase the tiles, and they can expect to sell x = 150 tile sets in a month’s time. Since the problem asks for an answer in the form p = mx + b, they are assuming that the demand curve is a straight line going through the points (25,31) and (150, 6). The slope m is
And using point (25,31):
 -->  --> 
b. For a single product, you can find the revenue (R) by multiplying the quantity of the product sold, x, times the price, p. (R = xp).
Substitute the result you found from part a. into the equation R = xp to find the revenue equation. Provide your answer in simplified form.
d. and c. The costs of doing business can be found by adding fixed costs, such as rent, insurance, and wages, and variable costs, which are the costs to purchase the product you are selling. The portion of the company’s fixed costs allotted to this product is $600, and the supplier’s cost for a set of tile is $2 each. Let x represent the number of tile sets.
Find the cost equation for the tile sets. Write your answer in the form C = mx + b.
If b represents a fixed cost, what value would represent b?
The variable part is the cost for the tile sets not counting fixed costs;  (in $).
The fixed costs $600 is added to that.  represents those fixed costs.
The total cost,  (in $) to produce  sets of tiles is
So the profits, 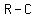 can be calculated as a function of as
We can find the number of tile sets, , needed to be sold for the maximum of that quadratic function  and figure out how to price the sets of tile to get that sales figure.
So let's set the price at $19 per tile set and hope that we got a good estimate with that demand equation/curve.
|
|
|
