|
Question 546397: the sum of the digits oa a two-digits number is 11. if the digits are reversed, the value of the new number is nine more than the value of the orginial number. what is the orginial number.
Answer by KMST(5328)   (Show Source):
You can put this solution on YOUR website! If reversing the digits adds 9, which is adding 10 and subtracting 1, it means that the new tens digit is one more than the other and the new ones digit is one less. In other words, in the original number the ones digit was one more that the tens digit. And if they add up to 11, the original number must have been 56, and reversing it gives you 65, which is 9 more.
However, the intention was probably to make you write equations, so here it goes.
Let t be the tens digit in the original number.
Let u be the units (ones) digit in the original number.
They add up to 11, so we write:
The value of the original number is  .
The value of the number made with the digits reversed is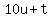 
Those two values are related by the equation
 <-->
Subtracting 10t and u from both sides we get
 , which dividing both sides by 9 gives us 
The system of equations:
can be solved whichever way you chose to yield  and  .
|
|
|
| |
