SOLUTION: Two sides of parallelogram are 68 and 83 inches and one of the diagonals is 42 inches. Find the angles of the parallelogram

Algebra ->  Polygons -> SOLUTION: Two sides of parallelogram are 68 and 83 inches and one of the diagonals is 42 inches. Find the angles of the parallelogram      Log On


   

Question 545828: Two sides of parallelogram are 68 and 83 inches and one of the diagonals is 42 inches. Find the angles of the parallelogram
Answer by Edwin McCravy(20060) About Me  (Show Source):
You can put this solution on YOUR website!
The parallelogram and diagonal are drawn to scale here: 



We have a case of side-side-side in triangle ABD, so we use 
the law of cosines solved for the cosine on triangle ABD:

The cosine of any given angle equals the sum of the squares of 
its sides minus the square of its opposite side, divided by twice
the product of its sides


cos(A) = %28AD%5E2%2BAB%5E2-BD%5E2%29%2F%282%2AAD%2AAB%29

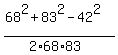cos(A) = %2868%5E2%2B83%5E2-42%5E2%29%2F%282%2A68%2A83%29

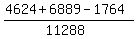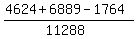cos(A) = %284624%2B6889-1764%29%2F%2811288%29

cos(A) = %289749%29%2F%2811288%29

cos(A) = %284624%2B6889-1764%29%2F%2811288%29

cos(A) = .86366052545

A = 30.26989518°

That's also the measure of angle C

Angles ABC and ADC are supplementary to angles A and C,
so their measures are:

180° - 30.26989518° = 149.7301048° each.

You can round off as you teacher told you, probably to
the nearst whole degree, which would be 30° and 150°.

Edwin