Question 545163: use the intermediate value theorem to determine whether the polynomial function has a zero in the given interval. please show work.
can someone please help!!
f(x)=8x^5-4x^3-9x^2-9; [1,2]
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! The function is a polynomial function, and polynomial functions are continuous. So your intermediate value theorem tells you that between x=1 and x=2, f(x) will take all the values between f(1) and f(2). For any value you pick, between f(1) and f(2), there will be a point x=c, where the function will take that value. (You can always calculate an approximation for that x=c, by trial and error, but it may not be easy, and you may not be able to calculate the exact value).


Since 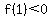 and and 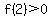 , , 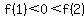 . .
In other words, zero is between f(1) and f(2).
So the function has to go through zero at some point in the interval (1,2).
If f(1) and f(2) were both positive, or both negative, you would not know if the function had a zero in (1,2).
|
|
|