Question 544991: I have a big problem with this equation.
5^(x-2) = 3^(2x)
That is,

I know the answer but I don't know what's the method to have it.
The answer is: log 25 / log 5/9
Help me please
Thank you
Found 2 solutions by stanbon, mseely:
Answer by stanbon(75887)   (Show Source): (Show Source):
You can put this solution on YOUR website! 5^(x-2) = 3^(2x)
---------------
(x-2)log(5) = (2x)log(3)
---
xlog(5) - log(25) = x(log(9))
----
x[log(5)-log(9)] = log(25)
---
x = log(25)/(log(5/9))
------
x = -5.4763
================
Cheers,
Stan H.
================
Answer by mseely(2)   (Show Source): (Show Source):
You can put this solution on YOUR website! The key word here is Exponential Equation. That means that the variable that you are solving for is located in exponent position.
The method for solving Exponential Equations is to apply the log function to both sides of the equation, that is, take the log of both sides of the equation. All Exponential Equations are solved this way.
Even with two exponential parts, as in this problem, the method is the same. Isolate each exponential part on opposite sides of the equal sign. In this problem, the two exponential parts, 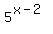 and and 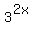 , are already isolated on opposite sides of the equal sign. , are already isolated on opposite sides of the equal sign.
So apply the log function to both sides of the equation, or "take the log of both sides."


Since we are now dealing with logs, this allows the possibility of the exponents containing your variable to "come down" into coefficient position. This is allowed by the Power Rule of logs.
Since by the Power Rule of logs,  can be rewritten as can be rewritten as 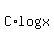 , we now have , we now have
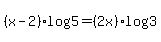
Now this is a linear equation in one variable, x, which can be solved by earlier methods. That is, isolate x. First, as always when solving a linear equation, clear parentheses.

Since x is on both sides of the equation, use the Addition or Subtraction Property of Equality to get both x terms on the same side.




Now, use the Addition or Subtraction Property of Equality to "move" any "non-x" terms to the other side of the equal sign.




Now combine the x terms, that is, combine like terms. In this case, it is easier to think of it as factoring out the common x factor, since the numbers are so ugly, involving logs. Remember that all these logs are just numbers, they are just coefficients of x like the 2 in 2x, for example. Still, we do not want to use our calculator to evaluate log(5) or log(3), for example, because we would have to round our answer--we want to leave them as logs and keep them exact.

Now that all x terms have been combined into one x term, continue to use linear equation solving methods to isolate x. Since something is being multiplied by x, we use the Division Property of Equality to divide it away. Remember, always identify the operation that exists, and then "do the opposite" operation.

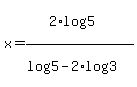
Now, to simplify our answer, we use any of the three log rules that may apply to combine all log expressions into the fewest number of log expressions as possible. First always apply the Power Rule of Logs to move any coefficients of logs back up into exponent position.


The use the Product Rule of Logs or the Quotient Rule of Logs to combine any sums or differences of logs that you see. Since by the Quotient Rule of Logs, 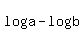 may be rewritten as may be rewritten as 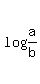 , ,


This is the exact answer desired. We never put our logs into a calculator to get a decimal answer which would have to be rounded, and therefore be imprecise.
To summarize, this was an Exponential Equation since our variable was in exponent position, which is always solved by isolating the exponential part of the equation as necessary, and taking the log of both sides. Then one uses strategies for Solving a Linear Equation, not being afraid of ugly expressions like 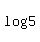 , which is just a number. , which is just a number.
|
|
|