|
Question 544669: I need help with this problem. It states that given that a parabola has a directrix of y= -3.25 and focus (0,-2.75), find the vertex. Then it wants me to write the equation of the parabola then graph the parabola.
Answer by lwsshak3(11628)   (Show Source): (Show Source):
You can put this solution on YOUR website! Given that a parabola has a directrix of y= -3.25 and focus (0,-2.75), find the vertex.
Write the equation of the parabola then graph the parabola.
**
Standard form of equation of given parabola: (x-h)^2=4p(y-k), (h,k)=(x,y) coordinates of vertex.
..
Since the given x-coordinate of the focus=0, the axis of symmetry is x=0.
And since the focus is above the directrix, the parabola opens upwards.
x-coordinate of vertex=x-coordinate of the focus=0
y-coordinate of vertex is midway between focus and directrix on the axis of symmetry:
(-3.25-2.75)/2=-6/2=-3
vertex:(0,3)
p=distance from vertex to focus or to directrix on the axis of symmetry=-3 to-2.75=.25
4p=.25=1/4
p=1/16
Equation of given parabola:
(x-0)^2=(1/16)(y+3)
x^2=(y+3)/16
..
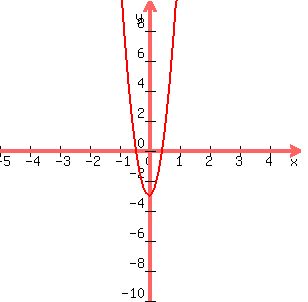
see graph below as a visual check on answers above:
y=16x^2-3
|
|
|
| |