Question 543871: In electronics, the state of a circuit element is described by two real numbers
(the voltage, V, across it, and the current, I, flowing through it). which (in
simplistic terms) describe its tendency to resist changes in voltage and current respectively.
These are much better described by complex numbers. Rather than the circuit
element's state having to be described by two different real numbers, V and I,
it can be described by a single complex number z = V + i*I
Similarly, inductance and capacitance can be thought of as the real and imaginary parts of another single complex number w = C + i*L
The laws of electricity can be expressed using complex addition and multiplication.
1) A given circuit has 9 volts flowing across it, and 3 amps of current flowing through it. We can express this as a single value, z = 9 + 3i. This same circuit has a capacitance of 7 farads and an inductance of 5 henries, this can also be expressed as a single value, w = 7 + 5i.
a) Combine z and w:
b) Find the product of z and w:
c) Divide z by w:
Answer by bucky(2189)   (Show Source): (Show Source):
You can put this solution on YOUR website! I wonder if any tutors other than me are going to tackle this one.
.
I find the introduction of the electronics as a source of complex numbers confusing, misleading, and, in some cases wrong. Complex numbers have always been used in describing the impedance of circuits, and the impedance is what relates the voltage to the current, both in magnitude and phase angle difference. The impedance is based on two factors, a real part called the resistance (R), and a complex part (the reactance (X)) which is based on the capacitance (C) and the inductance (L). For steady-state alternating current analysis the reactance generated by the circuit elements is:
.
 for capacitors and for capacitors and
 for inductors for inductors
.
Note that both of these reactances are dependent on f which is defined as the frequency of operation of the voltage source. Frequency is something that is not mentioned by the author of the problem.
.
The resistance of the circuit element is plotted on the horizontal (real) positive axis and the reactance is plotted on the imaginary (vertical) axis with the inductive reactance in the positive (upward) direction and the capacitive reactance in the negative (downward) direction.
.
What the author of the intended to do by presenting something outside of the standard method of handling such problems is questionable. (And to introduce 7 farad capacitors and 5 henry inductors may simplify the mathematics of the problem, but in general it doesn't reflect real world material properties.)
.
The point of all of this is just to ignore trying to understand the electronics and just concentrate on what you are asked to do with the two complex numbers contained in the problem. That's the lesson worth learning in this problem. The two complex numbers are:
.
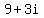 and and

.
You are asked first to combine these two numbers. (Presumably meaning to add them.) Do that by adding the real parts  and then adding the imaginary parts and then adding the imaginary parts  to get the answer to get the answer 
.
Next you are asked to find the product of these two numbers. Do this by the FOIL multiplication method:
.

.
The 
The 
The  and finally and finally
The  but remember that but remember that  so this answer is so this answer is 
.
and the combined result is 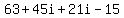 . Combining/adding the two real parts (63 - 15) and the two imaginary parts (45i + 21i) simplifies this product to the final answer of . Combining/adding the two real parts (63 - 15) and the two imaginary parts (45i + 21i) simplifies this product to the final answer of 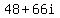
.
Finally, you are asked to divide (9 + 3i) by (7 + 5i).
.

.
Begin by recalling that the product of 
.
Apply that format to the denominator of this division ... that is multiply the denominator by 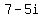 . (7 - 5i is called the conjugate of 7 + 5i, meaning it has the same two terms, but a different sign between them.) You can do this by multiplying both the numerator and the denominator by . (7 - 5i is called the conjugate of 7 + 5i, meaning it has the same two terms, but a different sign between them.) You can do this by multiplying both the numerator and the denominator by 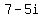 and this is equivalent to multiplying the fraction by 1. So: and this is equivalent to multiplying the fraction by 1. So:
.

.
Notice that multiplying the denominators (using the A & B rule above) results in the difference in the squares of the two terms. FOIL multiply the two numerators and the problem becomes:
.

.
This becomes:
.
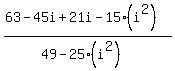
.
Again recall that by definition  . Substitute -1 for . Substitute -1 for  in the numerator and also in the denominator and get: in the numerator and also in the denominator and get:
.

.
You now divide both terms in the numerator by 74:
.

.
That's the answer to the division problem. You could divide both terms by the denominator 37 to get a decimal answer of 
.
Hope this helps you see what you had to do for this problem. The lessons to be learned are:
.
1. Complex numbers have a real part and an imaginary part that has an associated "i".
.
2. For adding (or subtracting) complex numbers add to (or subtract from) the real numbers and other real numbers. Also add to (or subtract from) the imaginary numbers and the other imaginary numbers.
.
3. Multiply complex numbers by using the FOIL method (First numbers, Outside numbers, Inside numbers, then Last numbers).
.
4. To divide complex numbers, make the denominator a real number by multiplying it by its conjugate. When you do that, you also have to multiply the numerator by the same conjugate. Then divide the real denominator into both the real term in the numerator and the imaginary term in the numerator.
.
5. Remember that "i" squared is -1.
|
|
|